Big Ideas Integrated Math 2 Chapter 2 Review #16 Answer Key

Are you looking for the best resources to seek homework aid and practice well for the examinations? Then, this Large Ideas Math Algebra ii Answers Affiliate 2 Quadratic Functions guide is the all-time selection for you lot all. In this commodity, y'all get to notice topic-wise BIM Algebra 2 Ch 2 Quadratic Functions Exercise questions & answers, practices, quizzes, chapter review, chapter tests, cumulative assessments, etc. for better learnings. Do practice with the Large Ideas Math Algebra ii Answers Guide and kickstart your preparation. Below you will observe the quick links to refer exercise questions & other materials directly and prepare all the concepts thoroughly.

Big Ideas Math Book Algebra 2 Answer Fundamental Chapter two Quadratic Functions

Solving all homework & assignments questions can be unproblematic by referring to this BIM Book Algebra 2 Answer Cardinal. Too, you lot can larn all the complex concepts of Chapter ii Quadratic Functions with the help of the Big Ideas Math Algebra two Volume Solution Cardinal and can answer any type of questions related to Affiliate two Quadratic Functions circuitous topics. Brand use of these below bachelor BIM Book Algebra two Reply Cardinal Chapter two Quadratic Functions straight links and fix well to score skillful results in any examinations.

• Quadratic Functions Maintaining Mathematical Proficiency – Page 45
• Quadratic Functions Mathematical Practices – Page 46
• Lesson 2.1 Transformations of Quadratic Functions – Folio (48-54)
• Transformations of Quadratic Functions 2.1 Exercises – Page (52-54)
• Lesson 2.2 Characteristics of Quadratic Functions – Page (56-64)
• Characteristics of Quadratic Functions two.2 Exercises – Page (61-64)
• Quadratic Functions Study Skills Using the Features of Your Textbook to Prepare for Quizzes and Tests – Page 65
• Quadratic Functions ii.one – 2.2 Quiz – Page 66
• Lesson 2.three Focus of a Parabola – Page (68-74)
• Focus of a Parabola ii.three Exercises – Folio (72-74)
• Lesson 2.4 Modeling with Quadratic Functions – Page (76-82)
• Modeling with Quadratic Functions 2.4 Exercises – Page (80-82)
• Quadratic Functions Performance Job: Accident Reconstruction – Page 83
• Quadratic Functions Affiliate Review – Page (84-86)
• Quadratic Functions Affiliate Test – Page 87
• Quadratic Functions Cumulative Assessment – Page (88-89)

Quadratic Functions Maintaining Mathematical Proficiency

Find the 10-intercept of the graph of the linear equation.

Question 1.
y = 2x + 7

Question 1.
y = 2x + 7

Question 2.
y = -6x + 8

Question iii.
y = -10x – 36

Question four.
y = 3(x – 5)

Question 5.
y = -4(x + x)

Question vi.
3x + 6y = 24

Find the altitude between the two points.

Question 7.
(2, 5), (-4, 7)

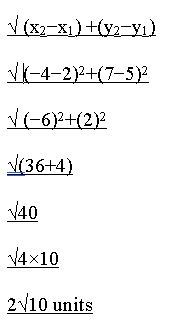
Question 8.
(-ane, 0), (-viii, four)

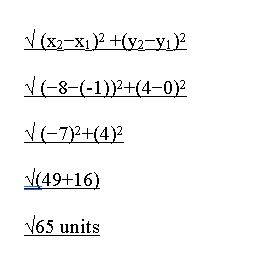
Question nine.
(three, 10), (5, ix)

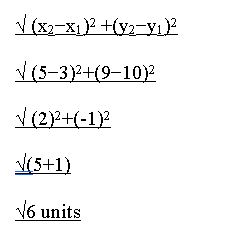
Question 10.
(7, -four), (-5, 0)

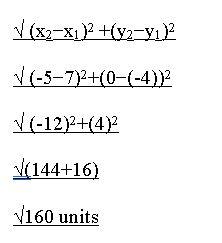
Question xi.
(iv, -8), (4, ii)

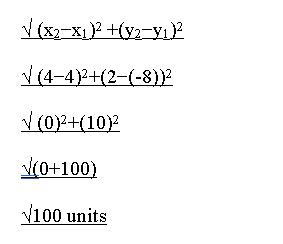
Question 12.
(0, 9), (-3, -6)

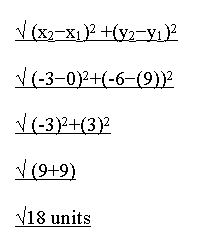
Question 13.
ABSTRACT REASONING Use the Distance Formula to write an expression for the distance between the two points (a, c) and (b, c). Is there an easier way to find the distance when the x-coordinates are equal? Explain your reasoning

Quadratic Functions Mathematical Practices

Monitoring Progress

Decide whether the syllogism represents correct or flawed reasoning. If flawed, explain why the determination is not valid.

Question ane.
All mammals are warm-blooded.
All dogs are mammals.
Therefore, all dogs are warm-blooded.

Question 2.
All mammals are warm-blooded.
My pet is warm-blooded.
Therefore, my pet is a mammal.

Question 3.
If I am sick, then I will miss school.
I missed school.
Therefore, I am ill.

Question four.
If I am ill, then I will miss schoolhouse.
I did non miss school.
Therefore, I am not sick.

Lesson 2.1 Transformations of Quadratic Functions

Essential Question

How practice the constants a, h, and 1000 impact the graph of the quadratic function g(x) = a(x – h)ⁱⁱ + yard?
The parent function of the quadratic family is f(x) = ten². A transformation of the graph of the parent function is represented past the function m(ten) = a(x – h)² + yard, where a ≠ 0.

EXPLORATION 1
Identifying Graphs of Quadratic Functions
Work with a partner. Match each quadratic function with its graph. Explicate your reasoning. Then apply a graphing estimator to verify that your answer is correct.
a. g(10) = -(x – 2)²
b. one thousand(x) = (x – 2)² + 2
c. 1000(x) = -(10 + 2)² – 2
d. g(x) = 0.5(x – 2)ⁱⁱ + 2
e. g(10) = 2(10 – 2)²
f. g(ten) = -(x + two)² + 2

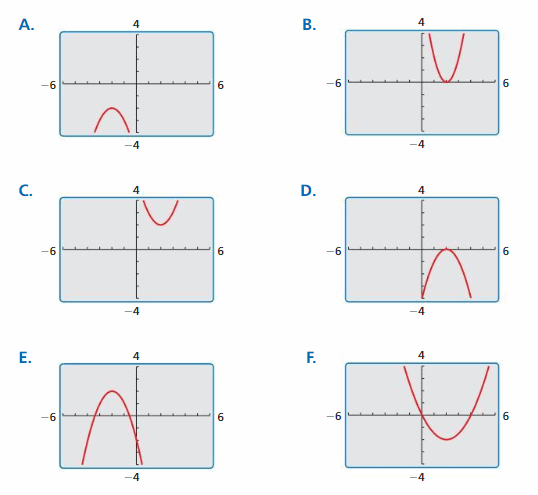
Communicate Your Answer

Question 2.
How do the constants a, h, and g impact the graph of the quadratic function g(10) =a(x – h)² + thou?

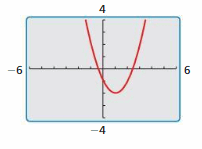
Question 3.
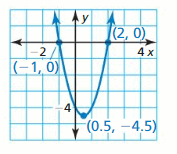
Write the equation of the quadratic function whose graph is shown at the right. Explain your reasoning. Then use a graphing calculator to verify that your equation is correct.

2.one Lesson

Monitoring Progress

Describe the transformation of f(x) = x² represented past chiliad. Then graph each part.

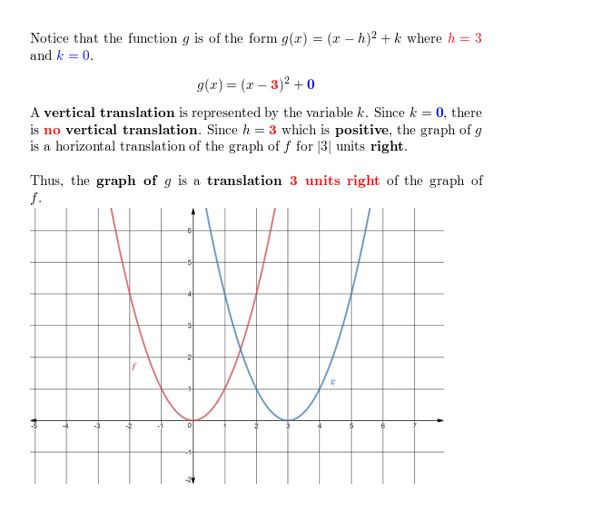
Question one.
thousand(x) = (x – 3)^two
Answer:

Question two.
grand(x) = (10 + 2)² – ii
Answer:

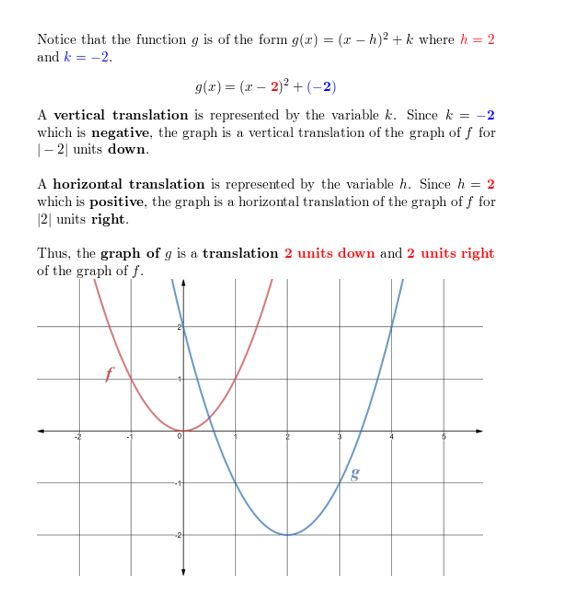
Question 3.
g(x) = (x + 5)² + 1
Respond:

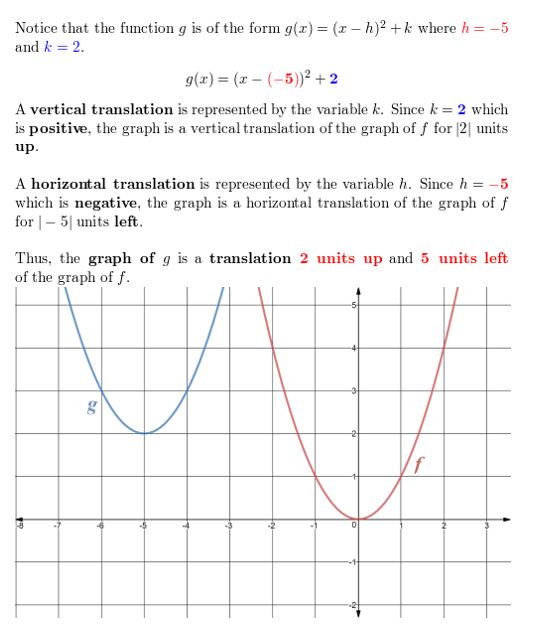
Describe the transformation of f(x) = 10ⁱⁱ represented past 1000. Then graph each function.

Question four.
chiliad(ten) = (\(\frac{1}{3} x\))^2
Answer:

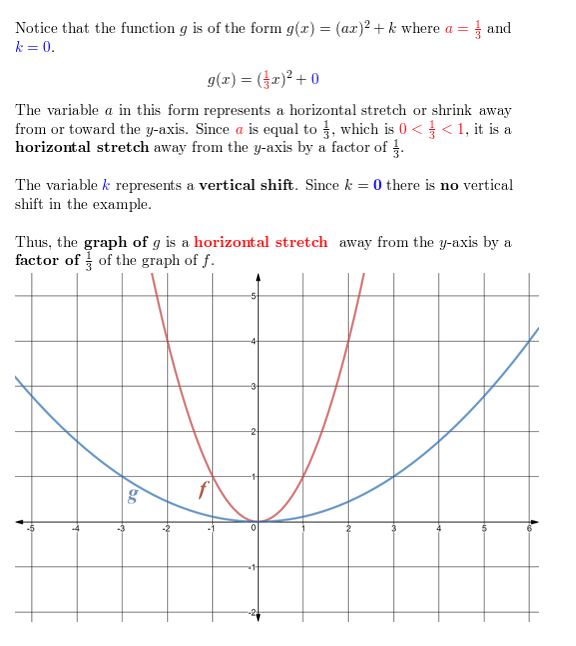
Question five.
thou(10) = 3(10 – one)^ii
Answer:

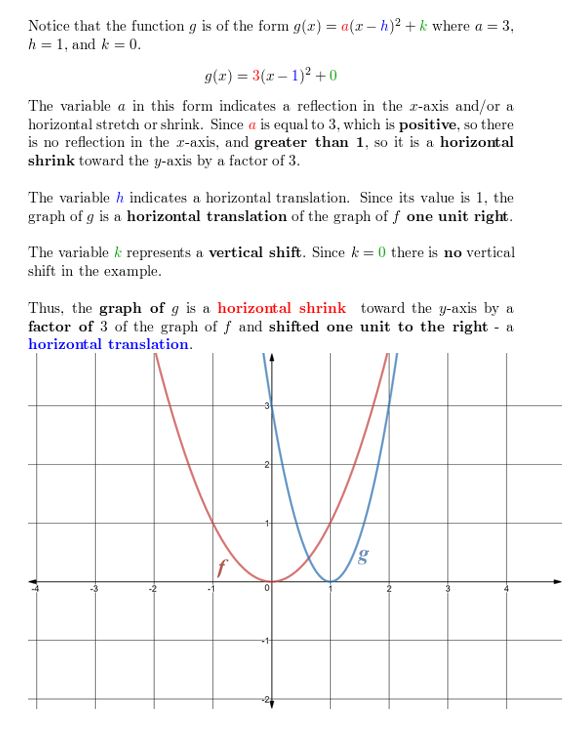
Question 6.
g(x) = -(x + 3)² + ii
Answer:

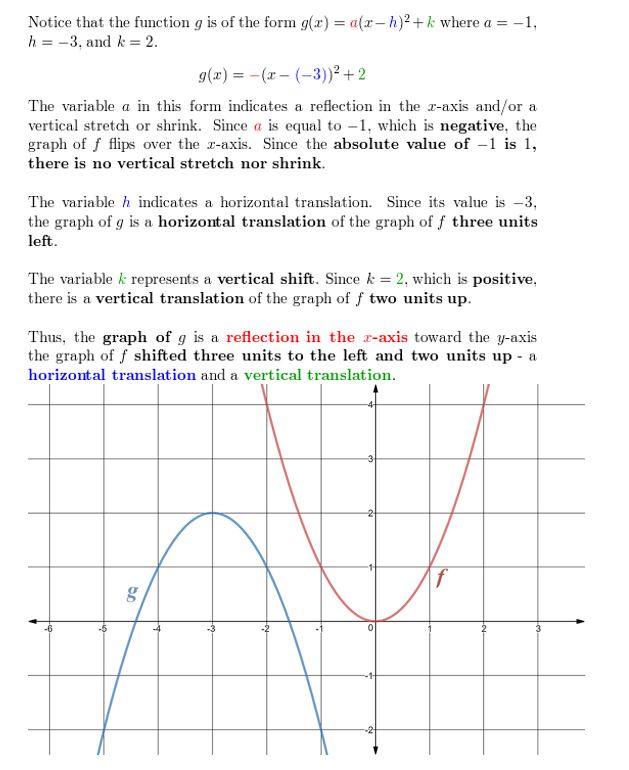
Question 7.
Permit the graph of g be a vertical shrink by a factor of \(\frac{1}{2}\) followed by a translation 2 units upwards of the graph of f(x) = ten². Write a rule for g and identify the vertex.

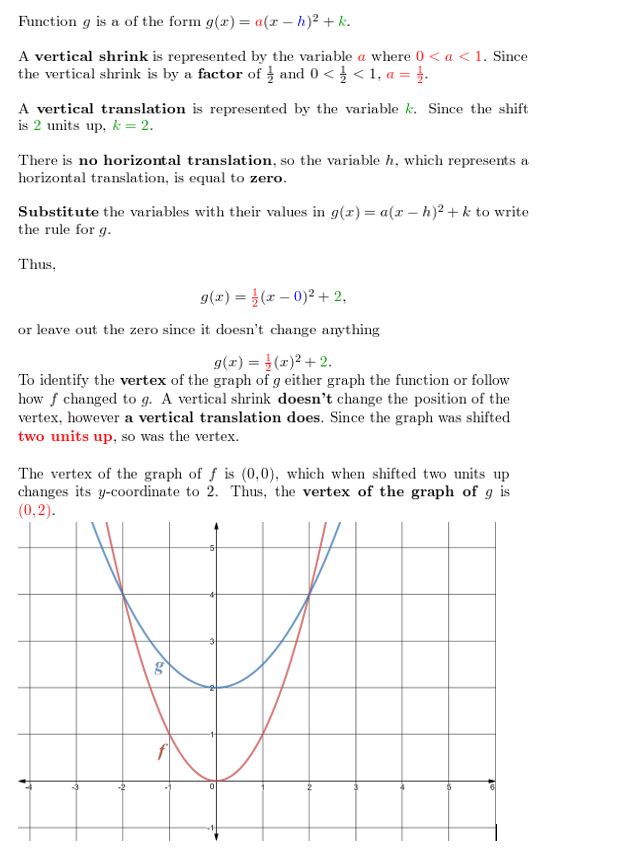
Question 8.
Let the graph of one thousand be a translation iv units left followed by a horizontal shrink by a factor of \(\frac{1}{three}\) of the graph of f(x) = x² + ten. Write a rule for k.

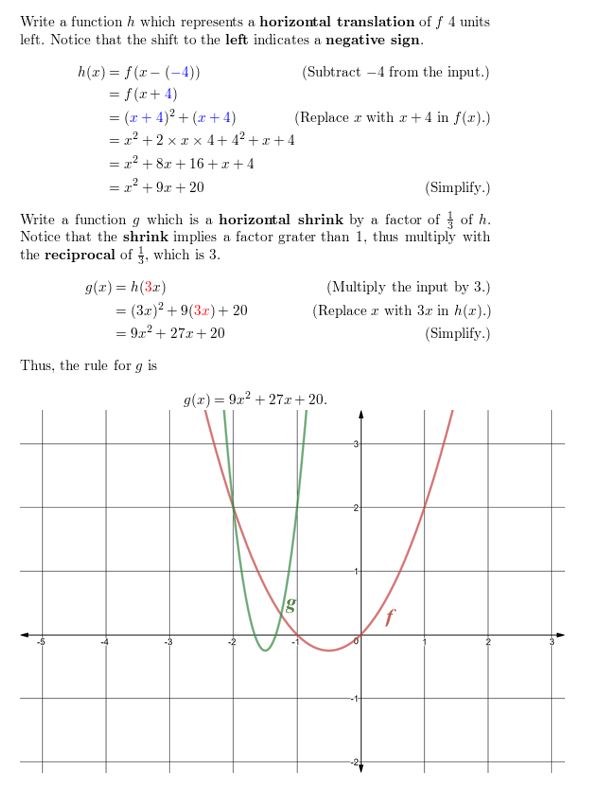
Question 9.
WHAT IF? In Example 5, the water hits the footing 10 feet closer to the fire truck after lowering the ladder. Write a office that models the new path of the water.

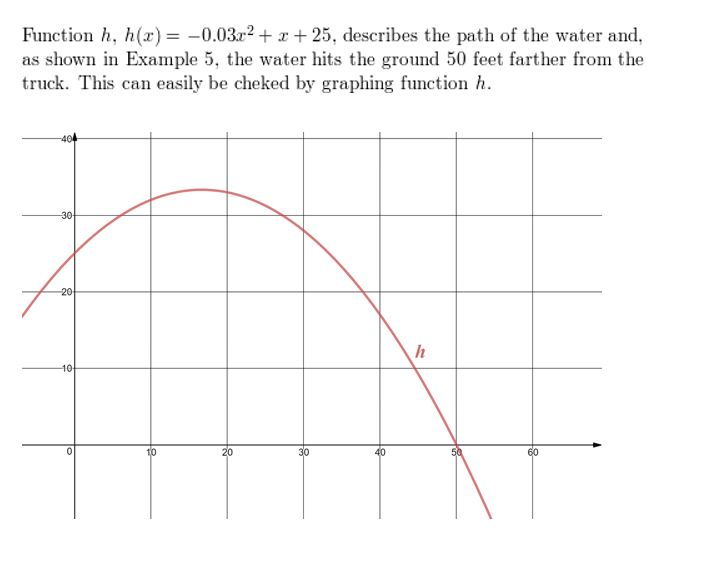
Transformations of Quadratic Functions 2.1 Exercises

Vocabulary and Core Concept Check

Question ane.
COMPLETE THE SENTENCE The graph of a quadratic function is chosen a(due north) ________.
Answer:

Question 2.
VOCABULARY Identify the vertex of the parabola given by f(x) = (x + 2)ⁱⁱ – iv.
Reply:

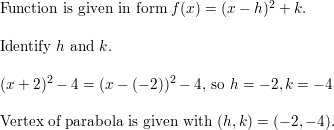
Monitoring Progress and Modeling with Mathematics

In Exercises iii–12, describe the transformation of f(10) = x² represented by chiliad. Then graph each function.

Question 3.
g(x) = xⁱⁱ – 3
Answer:

Question 4.
g(x) = x² + 1
Answer:

Question 5.
1000(ten) = (10 + 2)ⁱⁱ

Answer:

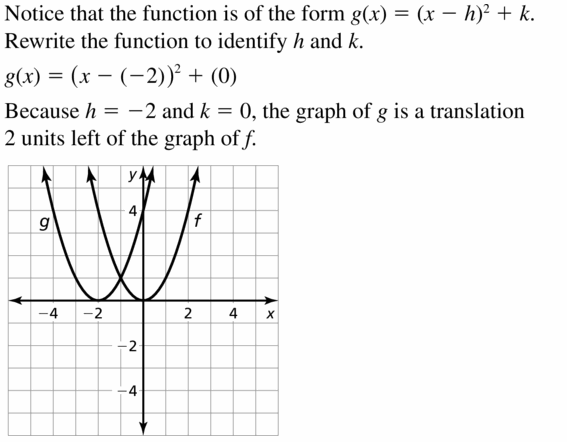
Question 6.
thou(x) = (x – iv)^two
Answer:

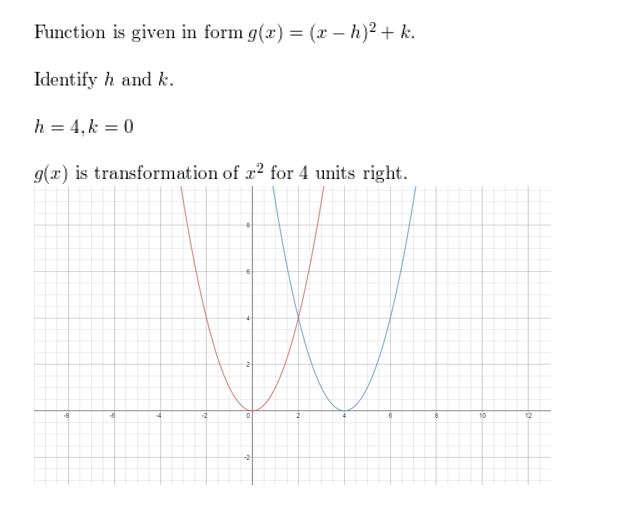
Question 7.
g(x) = (x – 1)²

Respond:

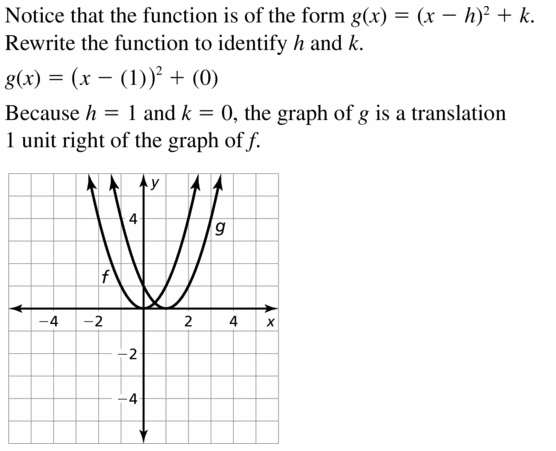
Question 8.
g(10) = (x + three)²

Answer:

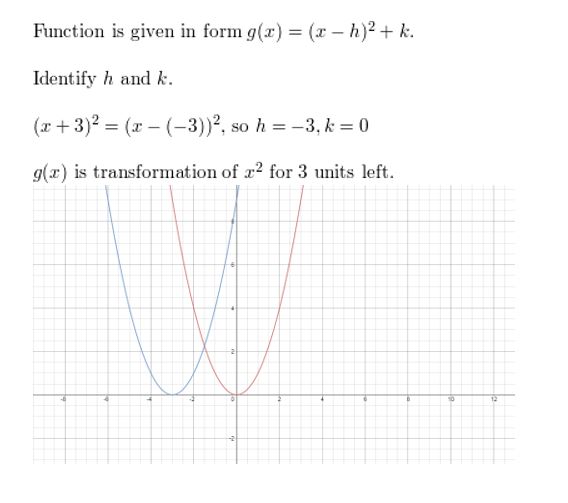
Question 9.
chiliad(x) = (x + 6)^two – ii
Answer:

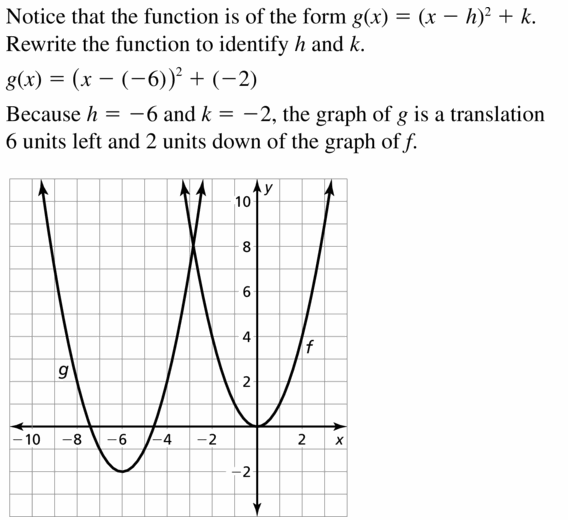
Question 10.
g(x) = (ten – ix)ⁱⁱ + 5
Reply:

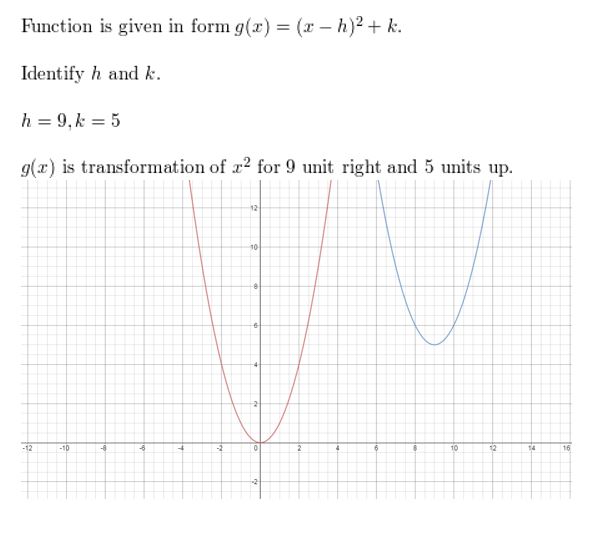
Question eleven.
grand(x) = (x – vii)ⁱⁱ + 1
Answer:

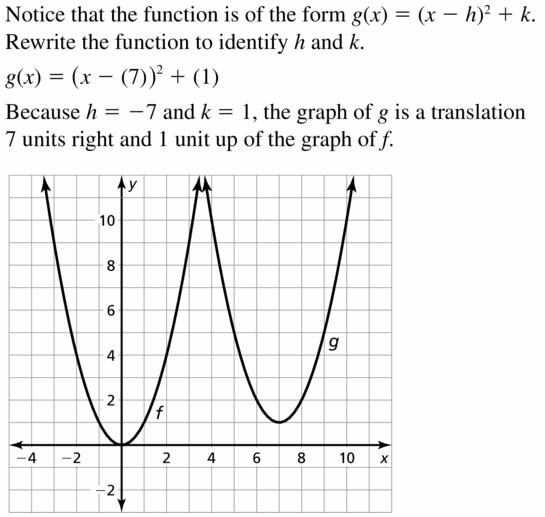
Question 12.
thou(x) = (x + ten)ⁱⁱ – 3
Answer:

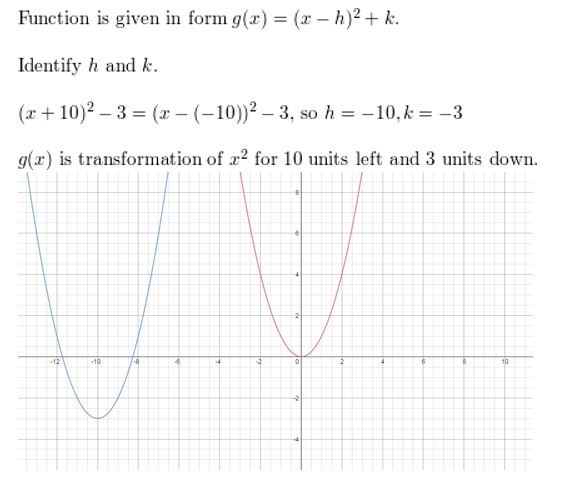
ANALYZING RELATIONSHIPS In Exercises thirteen–xvi, friction match the office with the correct transformation of the graph of f. Explain your reasoning.

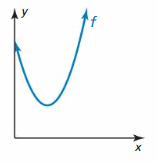
Question 13.
y = f(x – 1)
Respond:

Question 14.
y = f(10) + 1
Reply:

Question xv.
y = f(x – 1) + ane
Answer:

Question sixteen.
y = f(x + 1)
Answer:

In Exercises 17–24, describe the transformation of f(ten) = ten² represented by thousand. Then graph each function.

Question 17.
m(x) = -x²

Answer:

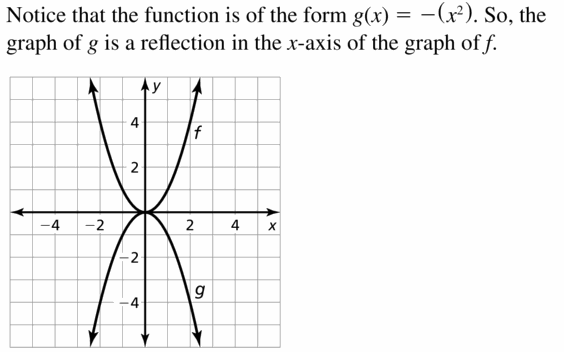
Question eighteen.
thousand(x) = (-x)²

Answer:

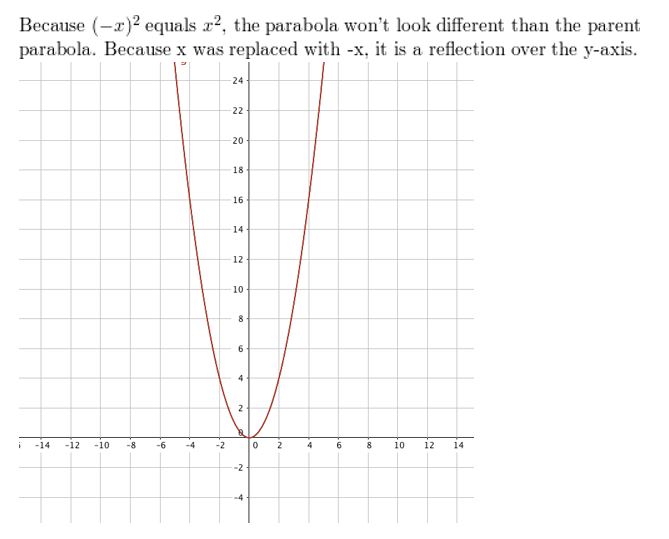
Question nineteen.
g(x) = 3x²

Answer:

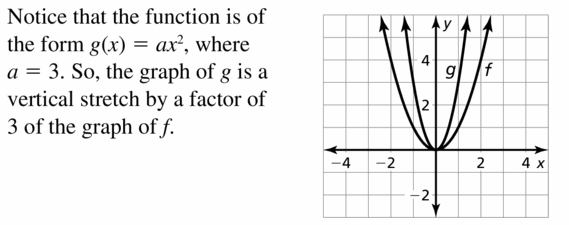
Question xx.
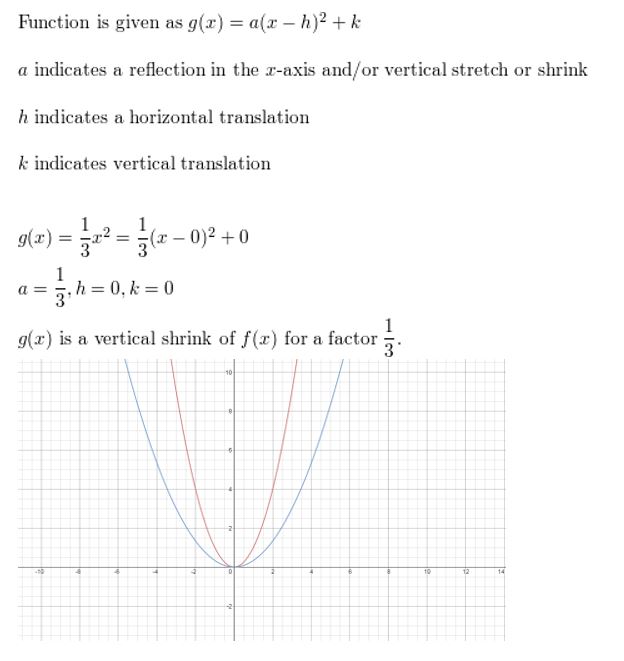
g(x) = \(\frac{i}{3}\)xⁱⁱ

Reply:

Question 21.
m(x) = (2x)²
Answer:

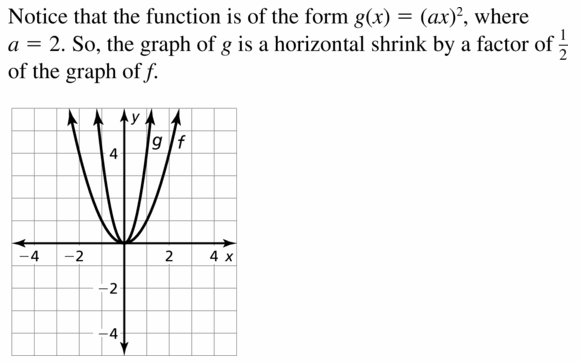
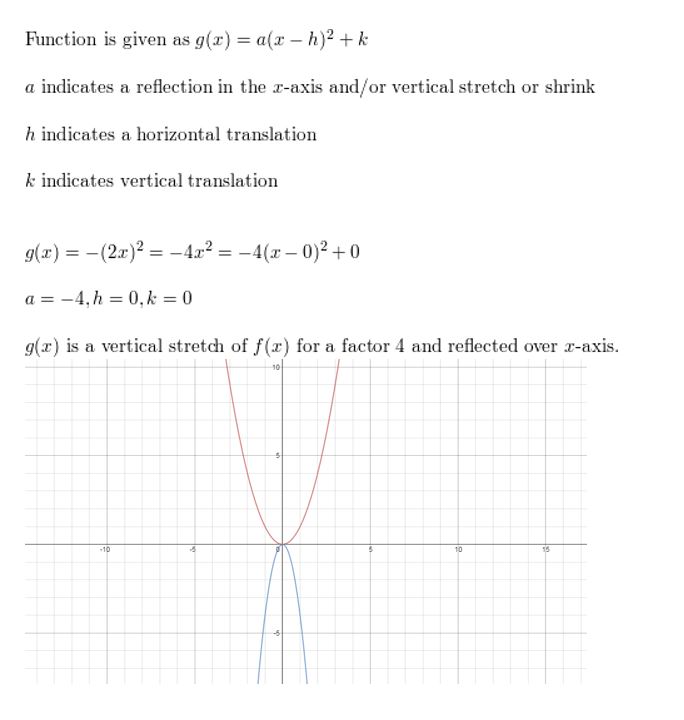
Question 22.
yard(x) = -(2x)²

Answer:

Question 23.
m(x) = \(\frac{1}{5}\)tenⁱⁱ – four
Respond:

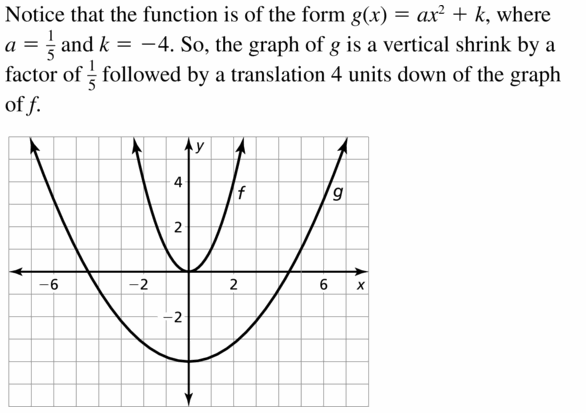
Question 24.
g(x) = \(\frac{i}{2}\)(x – 1)²

Reply:

Error ANALYSIS In Exercises 25 and 26, describe and right the error in analyzing the graph of f(ten) = −6x^two + 4.

Question 25.

Answer:

Question 26.

Reply:

USING Structure In Exercises 27–30, depict the transformation of the graph of the parent quadratic role. Then identify the vertex.

Question 27.
f(10) = 3(x + 2)² + 1
Answer:

Question 28.
f(x) = -iv(x + 1)² – five
Answer:

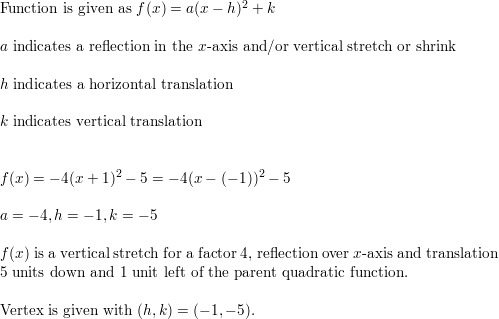
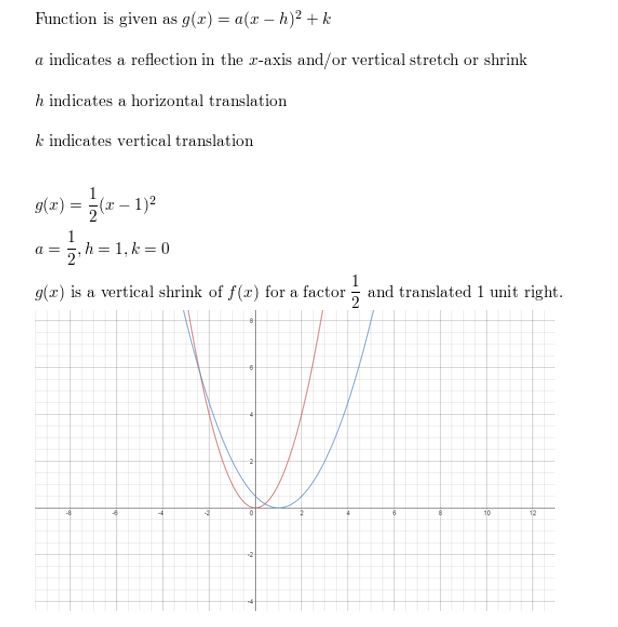
Question 29.
f(x) = -2x^two + 5
Respond:

Question 30.
f(x) = \(\frac{1}{2}\)(x – 1)²
Reply:

In Exercises 31–34, write a rule for g described by the transformations of the graph of f. Then identify the vertex.

Question 31.
f(x) = x² vertical stretch by a factor of 4 and a reflection in the x-axis, followed by a translation two units up
Answer:

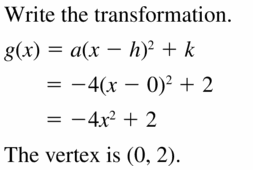
Question 32.
f(x) = 10²; vertical shrink past a factor of \(\frac{1}{three}\) and a reflection in the y-centrality, followed by a translation 3 units right
Answer:

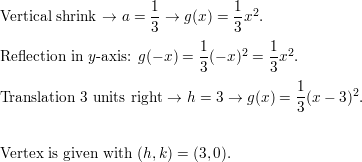
Question 33.
f(10) = 8x² – 6; horizontal stretch by a cistron of 2 and a translation ii units up, followed by a reflection in the y-axis
Answer:

Question 34.
f(x) = (x + 6)² + 3; horizontal shrink by a gene of \(\frac{1}{2}\) and a translation 1 unit down, followed by a reflection in the ten-axis
Respond:

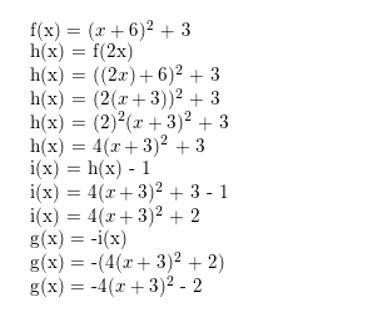
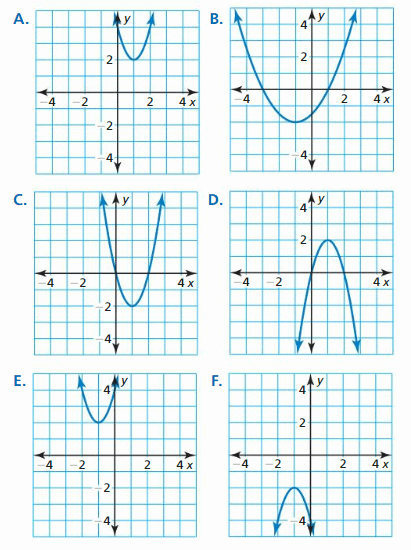
USING TOOLS In Exercises 35–forty, match the function with its graph. Explain your reasoning.

Question 35.
g(ten) = 2(x – i)² – 2
Respond:

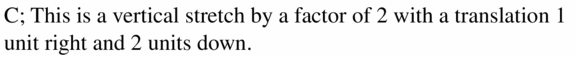
Question 36.
g(ten) = \(\frac{one}{2}\)(x + 1)² – 2
Answer:

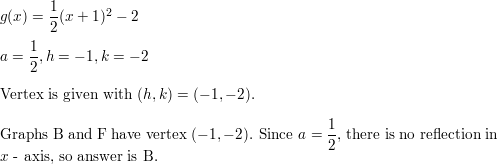
Question 37.
g(x) = -2(x – 1)² + 2
Answer:

Question 38.
g(ten) = 2(x + one)² + two
Respond:

Question 39.
yard(x) = -2(x + 1)² – 2
Respond:

Question twoscore.
chiliad(x) = 2(ten – 1)^two + 2
Reply:

JUSTIFYING STEPS In Exercises 41 and 42, justify eachstep in writing a part g based on the transformationsof f(x) = 2x² + 6x.

Question 41.
translation six units down followed by a reflection in the x-centrality

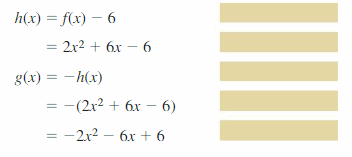
Answer:

Question 42.
reflection in the y-axis followed by a translation 4 units correct

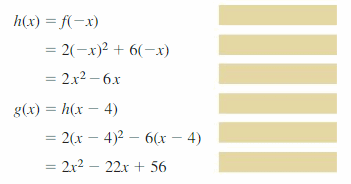
Answer:

Question 43.
MODELING WITH MATHEMATICS The function h(x) = -0.03(x – fourteen)ⁱⁱ + half-dozen models the jump of a crimson kangaroo, where x is the horizontal distance traveled (in anxiety) and h(ten) is the height (in feet). When the kangaroo jumps from a higher location, it lands 5 anxiety further away. Write a office that models the second bound.

Respond:

Question 44.
MODELING WITH MATHEMATICS The function f(t) = -16tⁱⁱ + ten models the height (in feet) of an object t seconds afterward it is dropped from a height of 10 feet on Earth. The same object dropped from the aforementioned height on the moon is modeled by g(t) = –\(\frac{viii}{3}\)tⁱⁱ + ten. Describe the transformation of the graph of f to obtain chiliad. From what height must the object be dropped on the moon and so it hits the ground at the same fourth dimension as on Earth?
Answer:

Question 45.
MODELING WITH MATHEMATICS Flying fish use their pectoral fins like plane wings to glide through the air.
a. Write an equation of the class y = a(x – h)ⁱⁱ + thou with vertex (33, 5) that models the flight path, assuming the fish leaves the water at (0, 0).
b. What are the domain and range of the function? What do they represent in this situation?
c. Does the value of a change when the flight path has vertex (30, 4)? Justify your answer.

Answer:

Question 46.
HOW Practise YOU Run across IT? Draw the graph of g as a transformation of the graph of f(x) = x².

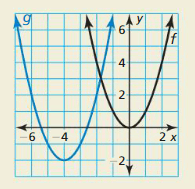
Answer:

Question 47.
COMPARING METHODS Let the graph of g be a translation 3 units upwards and 1 unit right followed by a vertical stretch past a gene of ii of the graph of f(x) = x^two.
a. Identify the values of a, h, and k and use vertex form to write the transformed office.
b. Use function notation to write the transformed function. Compare this function with your function in office (a).
c. Suppose the vertical stretch was performed kickoff, followed past the translations. Repeat parts (a) and (b).
d. Which method practise you prefer when writing a transformed function? Explain.
Answer:

Question 48.
THOUGHT PROVOKING A jump on a pogo stick with a conventional spring tin be modeled by f(ten) = -0.5(10 – 6)² + 18, where 10 is the horizontal altitude (in inches) and f(x) is the vertical distance (in inches). Write at least one transformation of the function and provide a possible reason for your transformation.
Answer:

Question 49.
MATHEMATICAL CONNECTIONS The area of a circle depends on the radius, as shown in the graph. A round earring with a radius of r millimeters has a circular pigsty with a radius of \(\frac{3 r}{four}\) millimeters. Describe a transformation of the graph below that models the area of the blue portion of the earring.

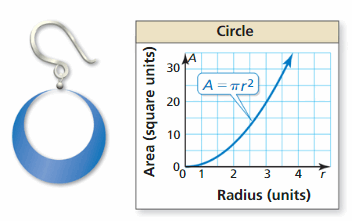
Answer:

Maintaining Mathematical Proficiency
A line of symmetry for the figure is shown in red. Detect the coordinates of point A. (Skills Review Handbook)

Question l.

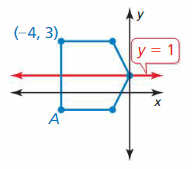
Reply:

Question 51.

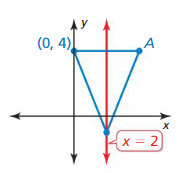
Answer:

Question 52.

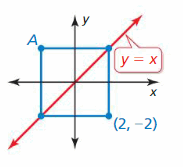
Answer:

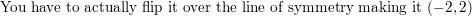
Lesson 2.2 Characteristics of Quadratic Functions

Essential Question
What type of symmetry does the graph of f(x) = a(ten – h)² + g take and how can you describe this symmetry?

EXPLORATION 1
Parabolas and Symmetry
Work with a partner.
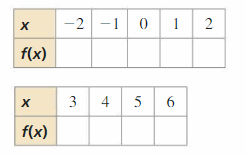
a. Consummate the tabular array. Then employ the values in the tabular array to sketch the graph of the role
f(10) = \(\frac{one}{2}\)x^two – 2x – 2 on graph newspaper.


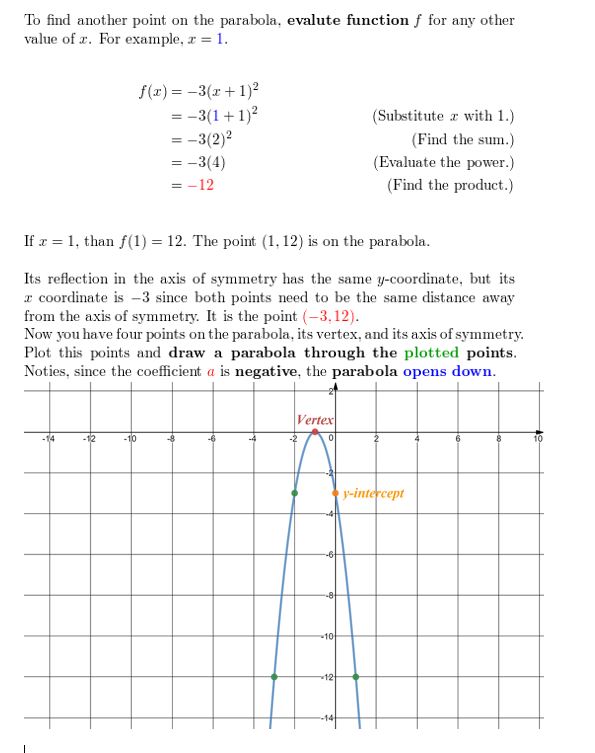
b. Use the results in role (a) to identify the vertex of the parabola.
c. Observe a vertical line on your graph newspaper and so that when you fold the paper, the left portion of the graph coincides with the right portion of the graph. What is the equation of this line? How does information technology relate to the vertex?

d. Show that the vertex course f(10) = \(\frac{1}{2}\)(x – 2)² – 4 is equivalent to the role given in part (a).

EXPLORATION 2
Parabolas and Symmetry
Work with a partner. Repeat Exploration 1 for the role given past f(x) = –\(\frac{one}{iii}\)x^two + 2x + 3 = –\(\frac{1}{3}\)(ten – 3),sup>2 + six.

Communicate Your Respond

Question 3.

What blazon of symmetry does the graph of f(ten) = a(ten – h)² + k have and how can you depict this symmetry?

Question 4.
Draw the symmetry of each graph. And so use a graphing calculator to verify your respond.
a. f(ten) = -(x – 1)ⁱⁱ + four
b. f(x) = (x + 1)² – ii
c. f(x) = two(x – three)² + 1
d. f(x) = \(\frac{1}{ii}\)(10 + ii)ⁱⁱ
e. f(ten) = -2x² + 3
f. f(10) = 3(x – v)^two + 2

ii.2 Lesson

Monitoring Progress

Graph the function. Label the vertex and centrality of symmetry.

Question 1.
f(x) = -3(10 + 1)ⁱⁱ

Question ii.
g(ten) = 2(x – ii)² + 5

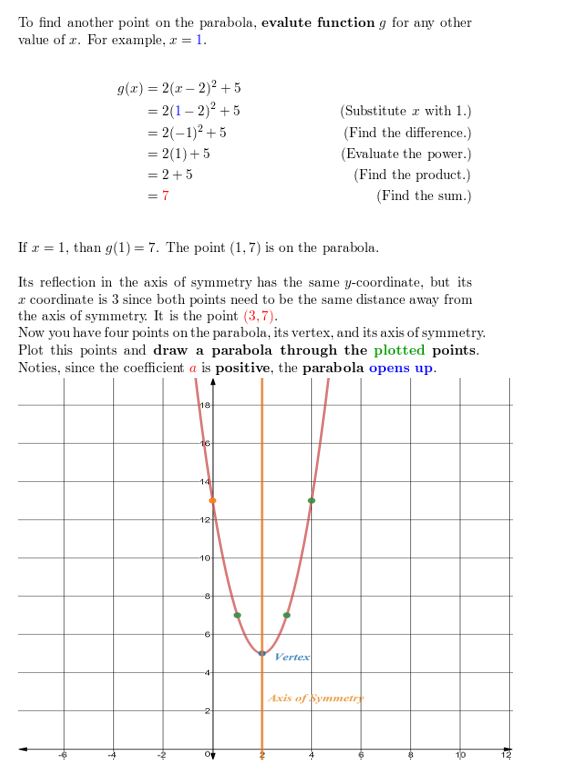
Question 3.
h(x) = ten² + 2x – 1

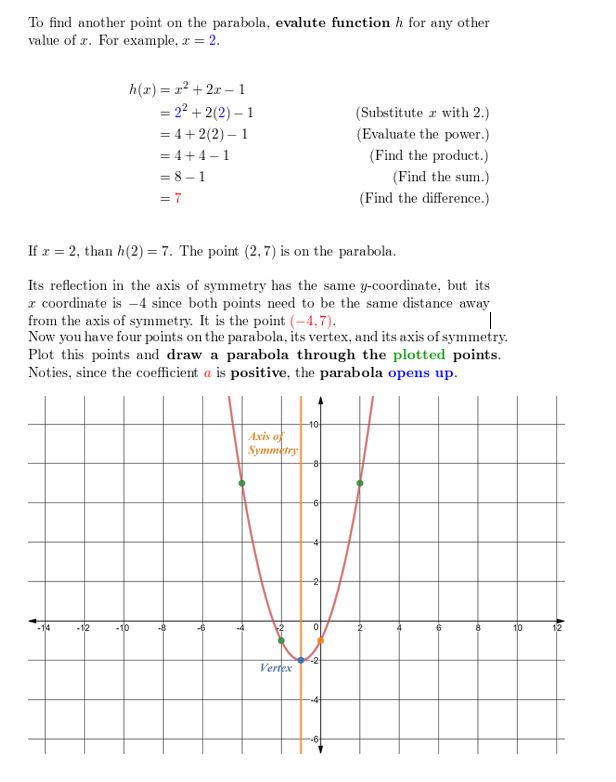
Question four.
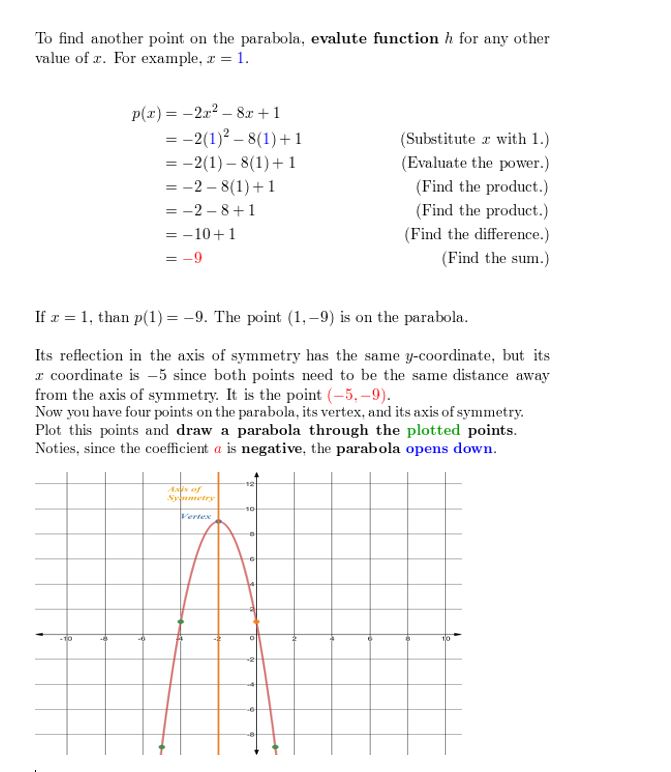
p(x) = -2xⁱⁱ – 8x + 1

Question v.
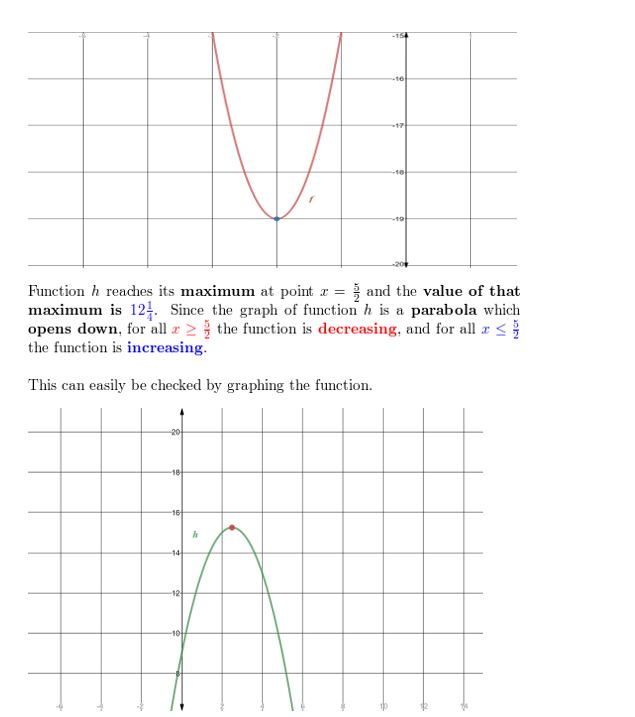
Observe the minimum value or maximum value of
(a) f(ten) = 4x² + 16x – 3 and
(b) h(x) = -xⁱⁱ + 5x + 9. Describe the domain and range of each function, and where each function is increasing and decreasing.

Graph the function. Label the x-intercepts, vertex, and axis of symmetry.

Question 6.
f(x) = -(x + 1)(ten + 5)

Question 7.
k(10) = \(\frac{i}{4}\)(10 – 6)(10 – 2)

Question 8.
WHAT IF? The graph of your 3rd shot is a parabola through the origin that reaches a maximum pinnacle of 28 yards when x = 45. Compare the distance it travels before it hits the ground with the distances of the beginning 2 shots.

Characteristics of Quadratic Functions 2.2 Exercises

Vocabulary and Core Concept and Check

Question ane.
WRITING Explain how to make up one's mind whether a quadratic function will have a minimum value or a maximum value.
Answer:

Question 2.
WHICH Ane DOESN'T BELONG? The graph of which function does not belong with the other three? Explain.

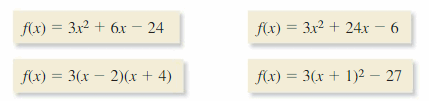
Answer:

Question 3.
f(x) = (x – 3)²
Answer:

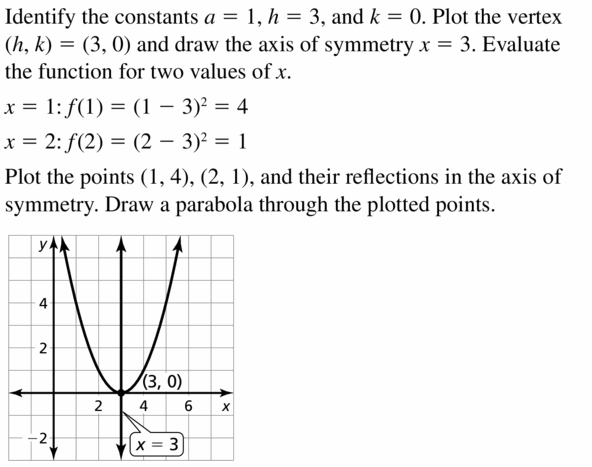
Question 4.
h(ten) = (x + 4)ⁱⁱ
Reply:

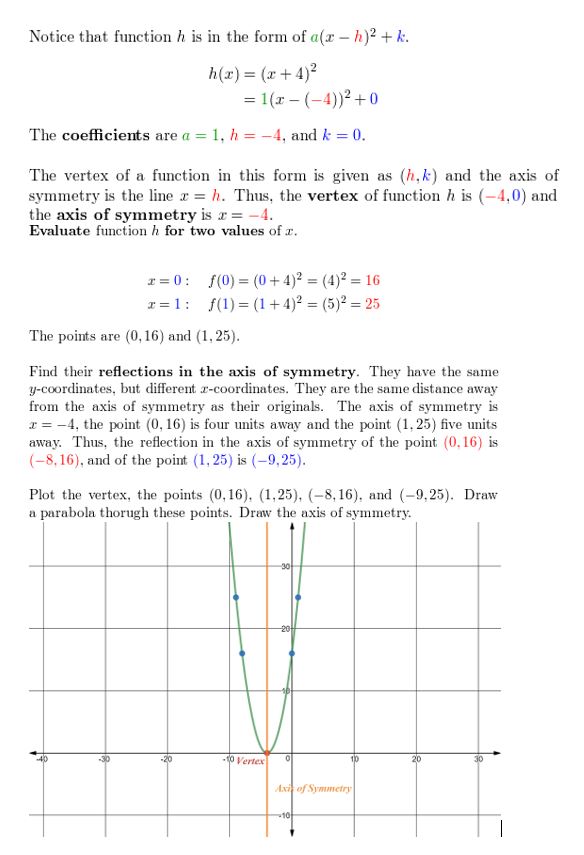
Question 5.
g(10) = (ten + three)² + v
Answer:

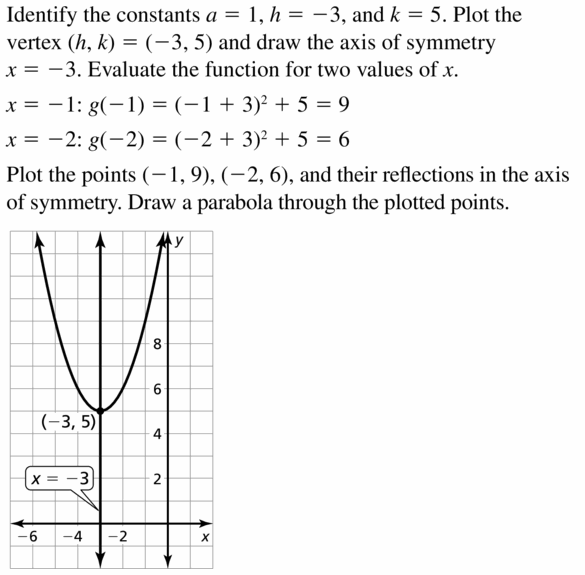
Question six.
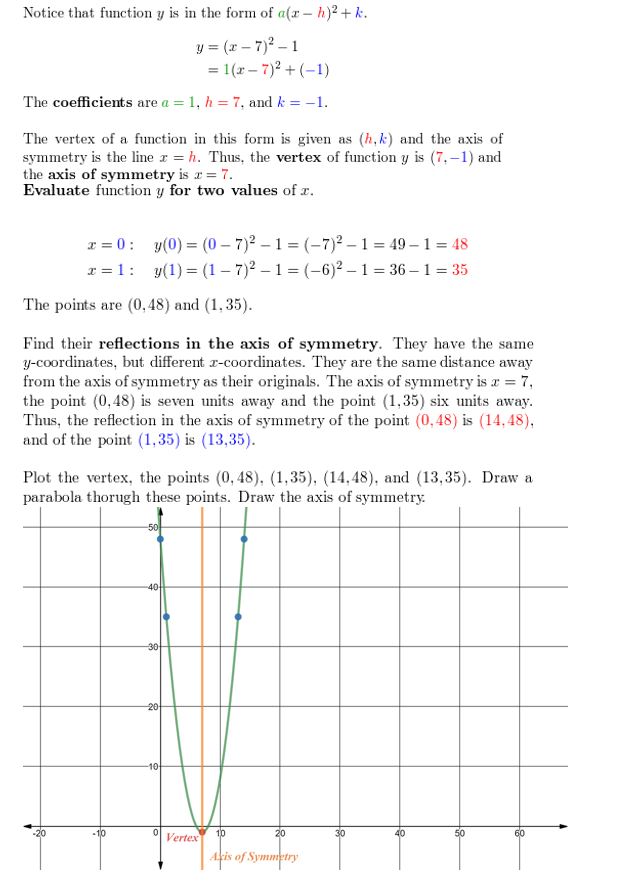
y = (x – 7)² – 1
Answer:

Question 7.
y = -iv(x – two)² + 4
Reply:

Question viii.
thousand(x) = ii(x + ane)² – iii
Respond:

Question nine.
f(x) = -ii(x – i)² – 5
Reply:

Question 10.
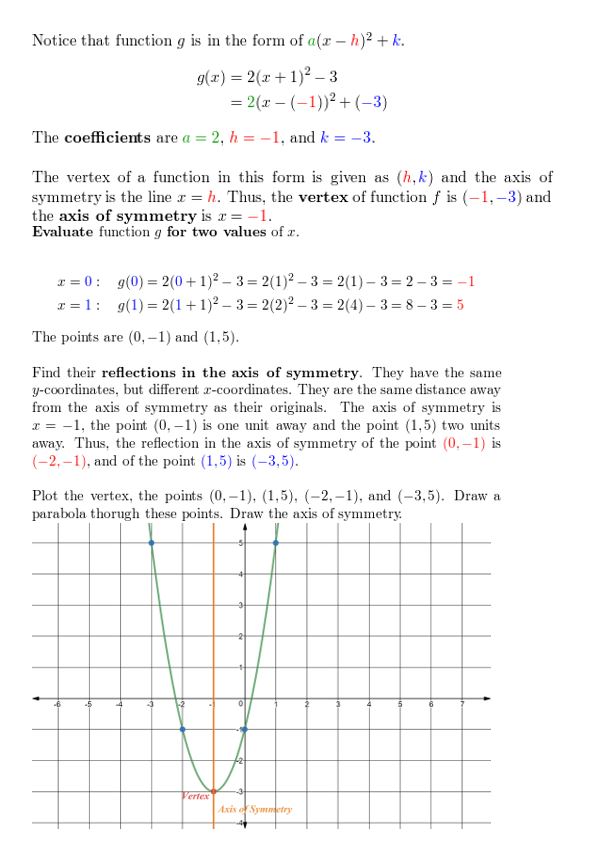
h(x) = 4(10 + iv)² + vi
Answer:

Question 11.
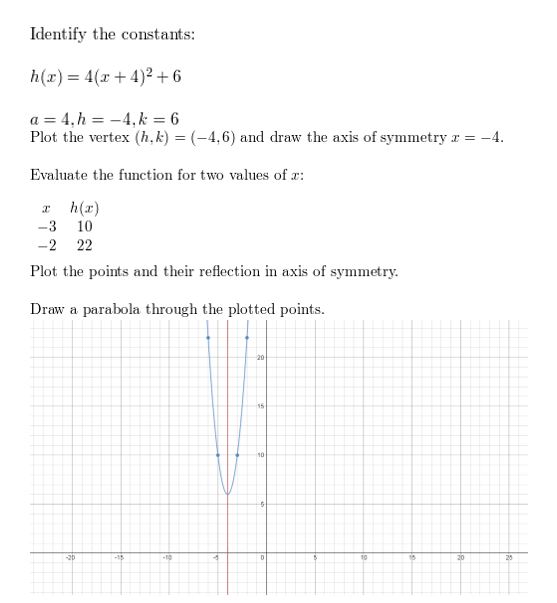
y = –\(\frac{1}{4}\)(x + 2)² + 1
Answer:

Question 12.
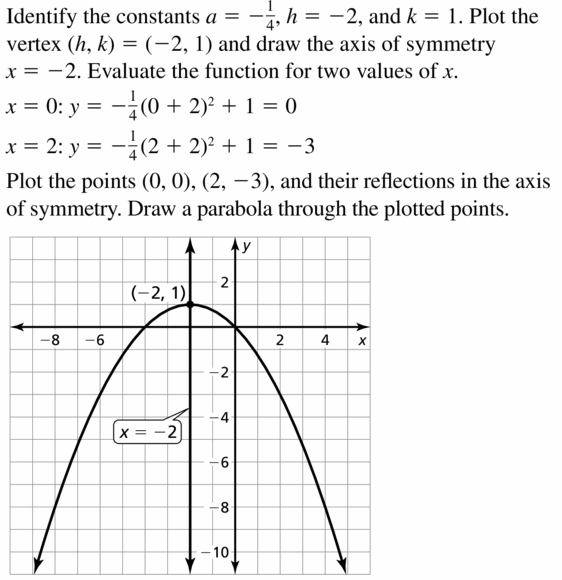
y = \(\frac{1}{two}\)(x – 3)² + two
Answer:

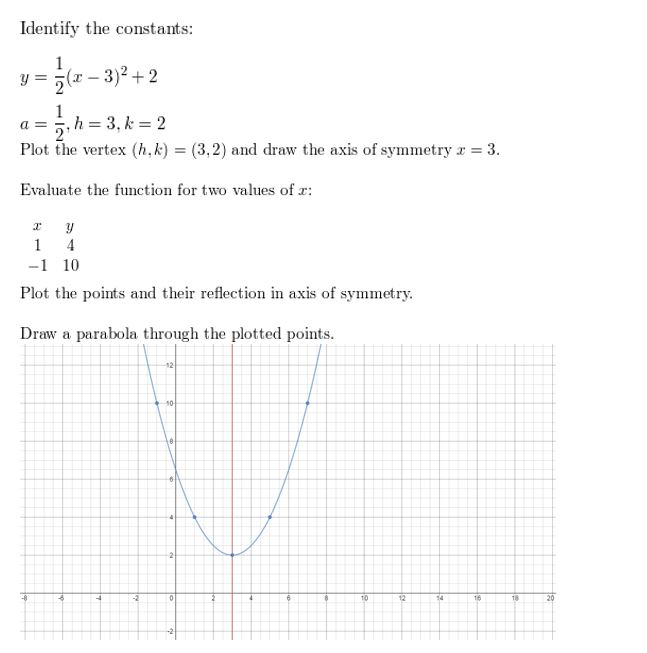
Question 13.
f(x) = 0.four(ten – 1)²
Reply:

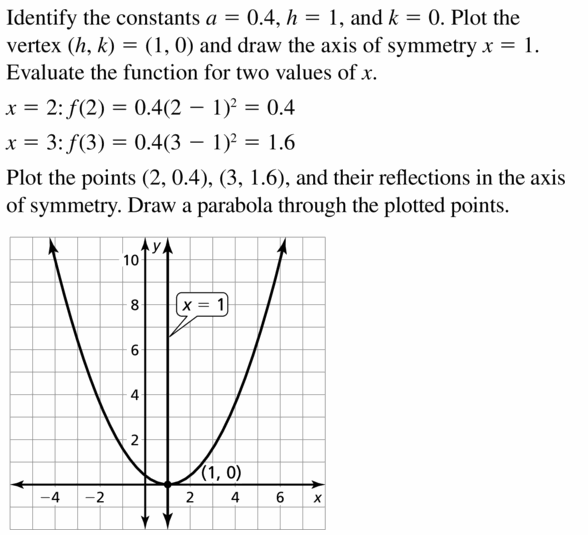
Question 14.
yard(10) = 0.75x^two – five
Answer:

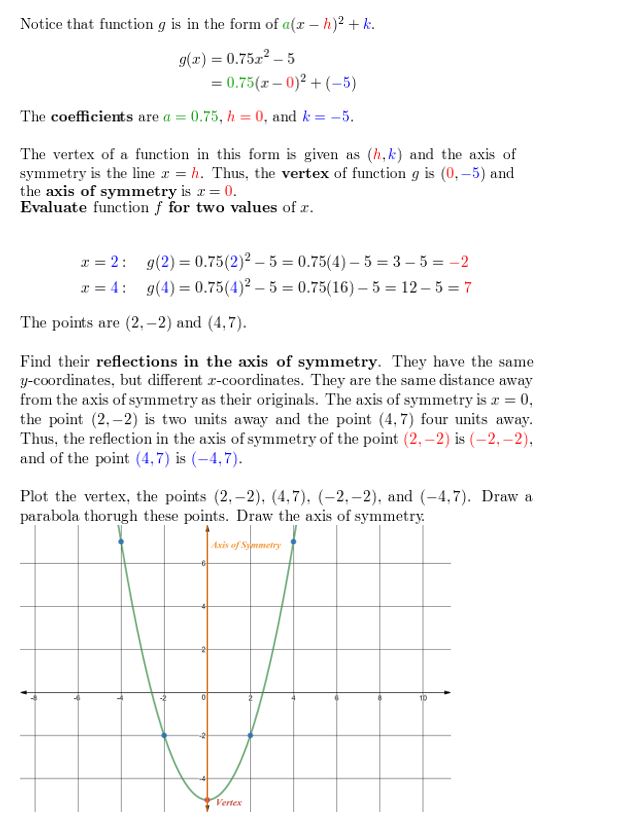
ANALYZING RELATIONSHIPS In Exercises xv–18, utilize the centrality of symmetry to match the equation with its graph.

Question 15.
y = ii(10 – 3)ⁱⁱ + 1
Respond:

Question 16.
y = (10 + 4)ⁱⁱ – 2
Answer:

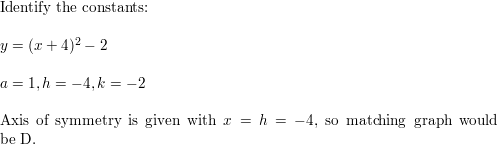
Question 17.
y = \(\frac{1}{2}\)(ten + ane)² + iii
Reply:

Question 18.
y = (10 – 2)² – ane

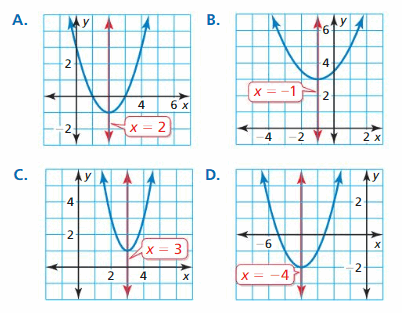
Answer:

REASONING In Exercises 19 and xx, utilize the centrality of symmetry to plot the reflection of each point and consummate the parabola.

Question nineteen.

Answer:

Question 20.

Answer:

In Exercises 21–thirty, graph the function. Label the vertex and axis of symmetry.

Question 21.
y = tenⁱⁱ + 2x + 1
Answer:

Question 22.
y = 3x^two – 6x + 4
Answer:

Question 23.
y = -4x² + 8x + 2
Reply:

Question 24.
f(10) = -x² – 6x + 3
Respond:

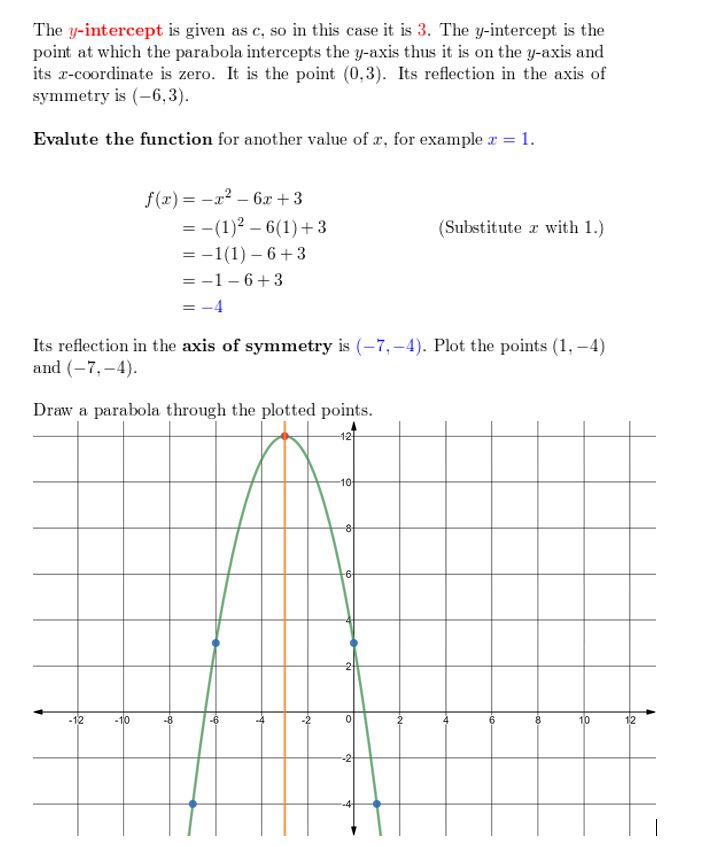
Question 25.
g(ten) = -x² – 1
Answer:

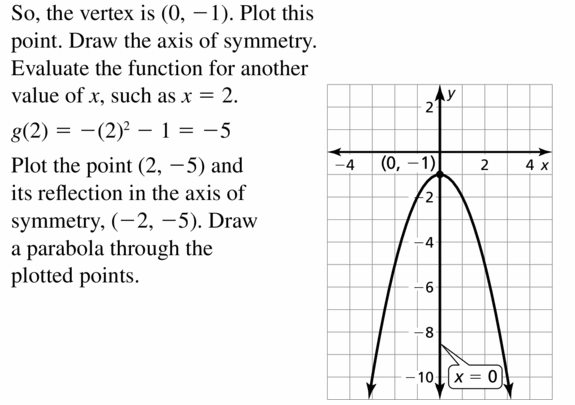
Question 26.
f(ten) = 6x² – v
Reply:

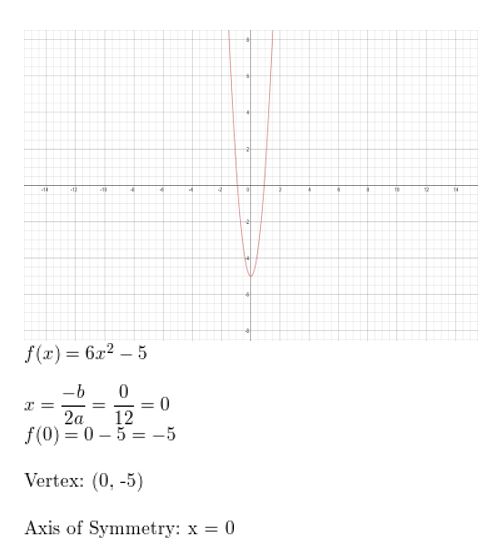
Question 27.
thousand(10) = -one.5xⁱⁱ + 3x + 2
Respond:

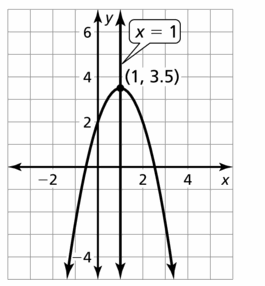
Question 28.
f(x) = 0.5x^two + x – 3
Answer:

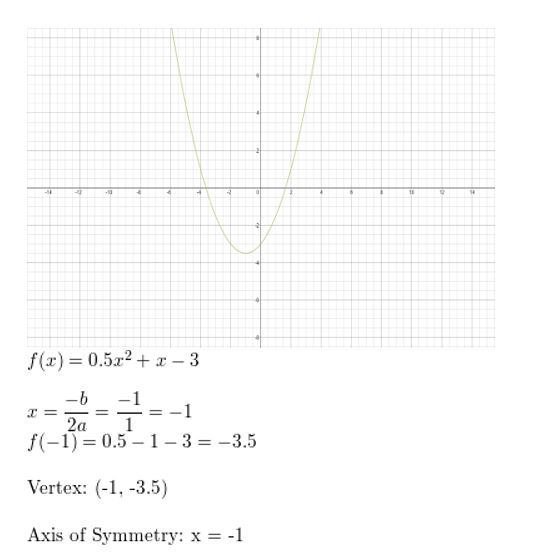
Question 29.
y = \(\frac{3}{2}\)x² – 3x + six
Answer:

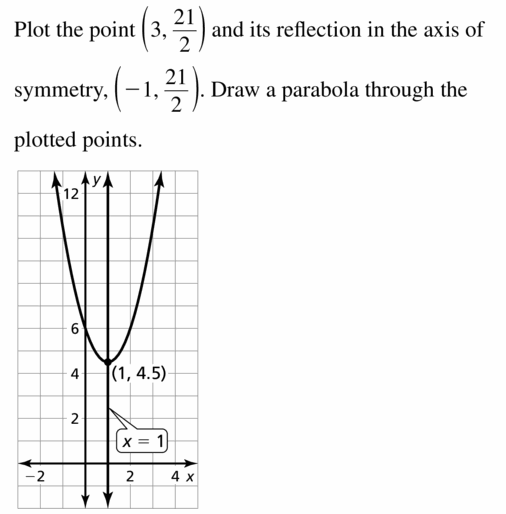
Question 30.
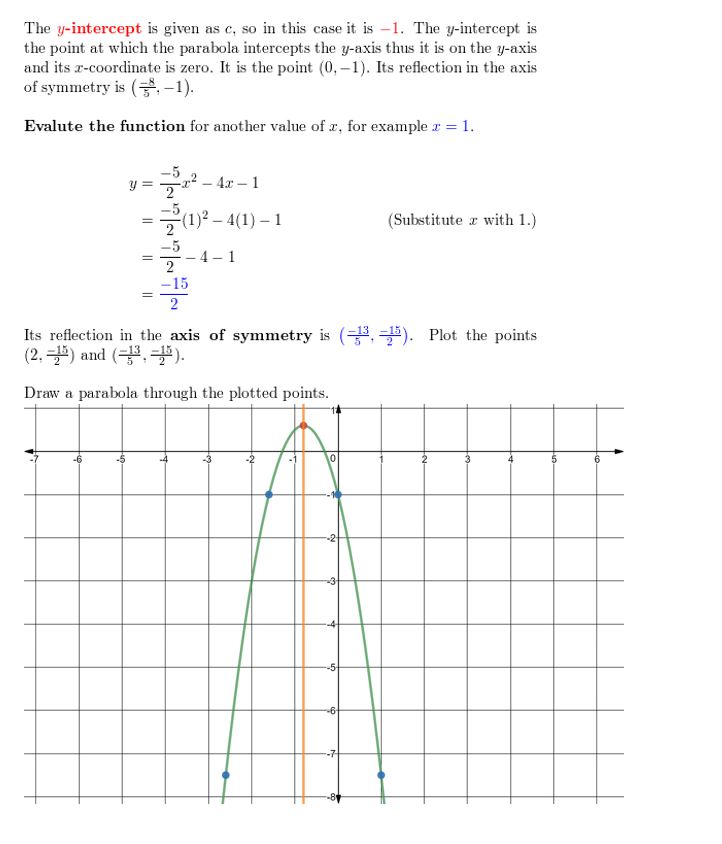
y = –\(\frac{5}{2}\)x² – 4x – 1
Respond:

Question 31.
WRITING Two quadratic functions have graphs with vertices (2, 4) and (2, -iii). Explain why you tin can non use the axes of symmetry to distinguish between the two functions.
Respond:

Question 32.
WRITING A quadratic function is increasing to the left of 10 = 2 and decreasing to the correct of ten = 2. Will the vertex exist the highest or everyman bespeak on the graph of the parabola? Explain.
Answer:

Mistake ANALYSIS In Exercises 33 and 34, describe and right the error in analyzing the graph of y = 4x² + 24x − 7.

Question 33.

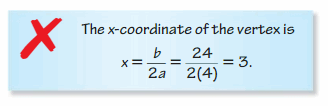
Answer:

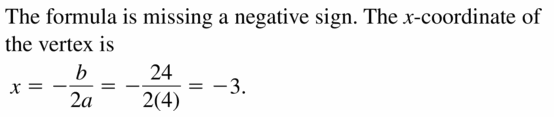
Question 34.

Reply:

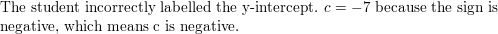
MODELING WITH MATHEMATICS In Exercises 35 and 36, x is the horizontal distance (in anxiety) and y is the vertical altitude (in feet). Observe and interpret the coordinates of the vertex.

Question 35.
The path of a basketball thrown at an angle of 45° can be modeled by y = -0.02x² + x + 6.
Reply:

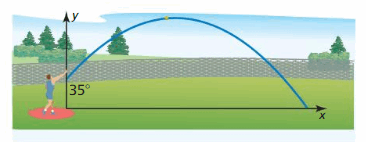
Question 36.
The path of a shot put released at an angle of 35° can be modeled by y = -0.01x² + 0.7x + half-dozen.

Answer:

Question 37.
ANALYZING EQUATIONS The graph of which function has the same axis of symmetry every bit the graph of y = x² + 2x + 2?
A. y = 2x² + 2x + ii
B. y = -3xⁱⁱ – 6x + 2
C. y = x² – 2x + 2
D. y = -5x² + 10x + 23
Answer:

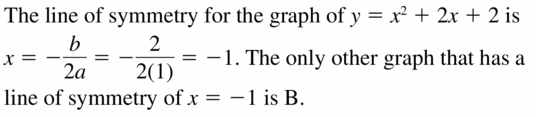
Question 38.
USING Structure Which function represents the widest parabola? Explain your reasoning.
A. y = 2(x + 3)²
B. y = xⁱⁱ – 5
C. y = 0.5(x – ane)² + 1
D. y = -10ⁱⁱ + six
Answer:

In Exercises 39–48, detect the minimum or maximum value of the role. Describe the domain and range of the function, and where the function is increasing and decreasing.

Question 39.
y = 6x^two – 1
Respond:

Question 40.
y = 9x^two + 7
Answer:

Question 41.
y = -xⁱⁱ – 4x – 2
Answer:

Question 42.
g(ten) = -3x² – 6x + 5
Answer:

Question 43.
f(x) = -2x² + 8x + vii
Respond:

Question 44.
g(x) = 3x² + 18x – 5
Respond:

Question 45.
h(ten) = 2x² – 12x
Answer:

Question 46.
h(x) = ten² – 4x
Answer:

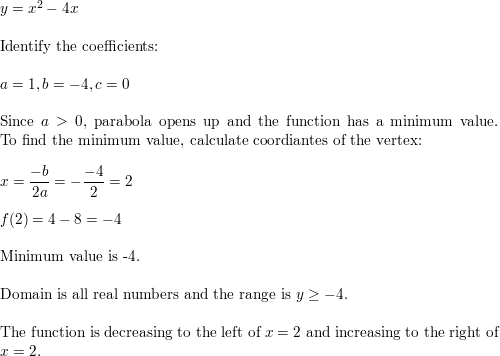
Question 47.
y = \(\frac{1}{4}\)x^two – 3x + 2
Answer:

Question 48.
f(x) = \(\frac{3}{2}\)x² + 6x + 4
Answer:

Question 49.
Problem SOLVING The path of a diver is modeled by the function f(x) = -9xⁱⁱ + 9x + one, where f(x) is the height of the diver (in meters) above the water and x is the horizontal distance (in meters) from the end of the diving board.
a. What is the height of the diving board?
b. What is the maximum height of the diver?
c. Describe where the diver is ascending and where the diver is descending.

Answer:

Question 50.
PROBLEM SOLVING The engine torque y (in foot-pounds) of one model of motorcar is given by y = -3.75xⁱⁱ + 23.2x + 38.viii, where x is the speed (in thousands of revolutions per minute) of the engine.
a. Discover the engine speed that maximizes torque. What is the maximum torque?
b. Explain what happens to the engine torque as the speed of the engine increases.
Respond:

MATHEMATICAL CONNECTIONS In Exercises 51 and 52, write an equation for the area of the figure. Then determine the maximum possible area of the figure.

Question 51.

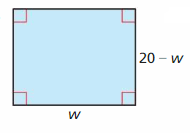
Answer:

Question 52.

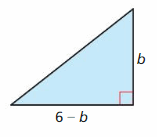
Respond:

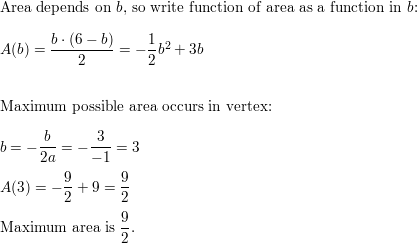
In Exercises 53–threescore, graph the function. Label the x-intercept(s), vertex, and axis of symmetry.

Question 53.
y = (x + three)(10 – iii)
Answer:

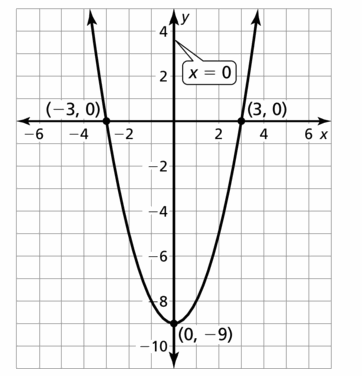
Question 54.
y = (x + 1)(x – 3)
Reply:

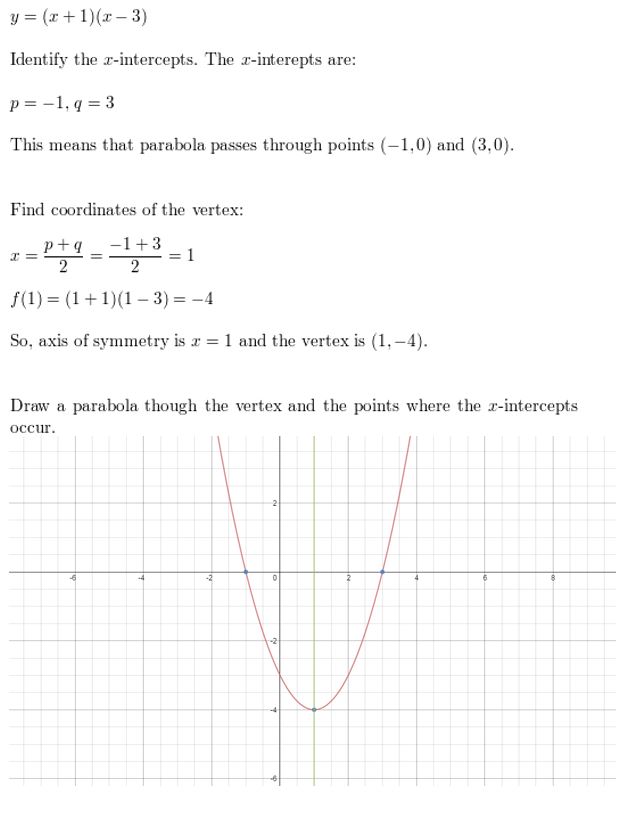
Question 55.
y = 3(x + 2)(x + half dozen)
Answer:

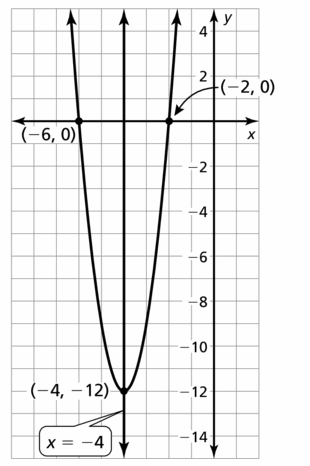
Question 56.
f(ten) = two(10 – five)(ten – 1)
Answer:

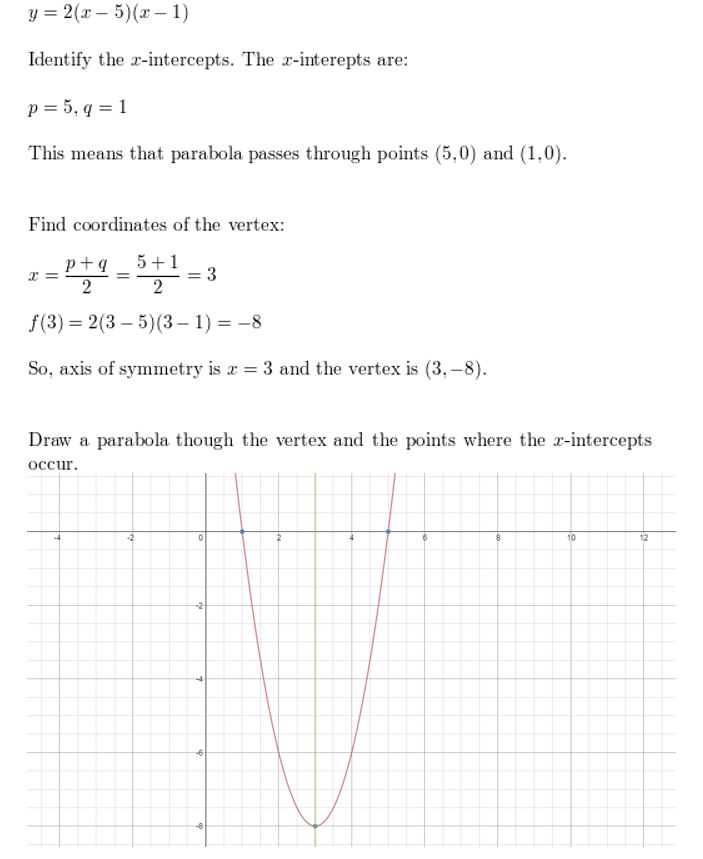
Question 57.
1000(x) = -x(x + vi)
Answer:

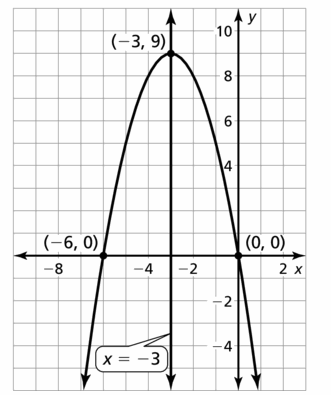
Question 58.
y = -4x(x + vii)
Respond:

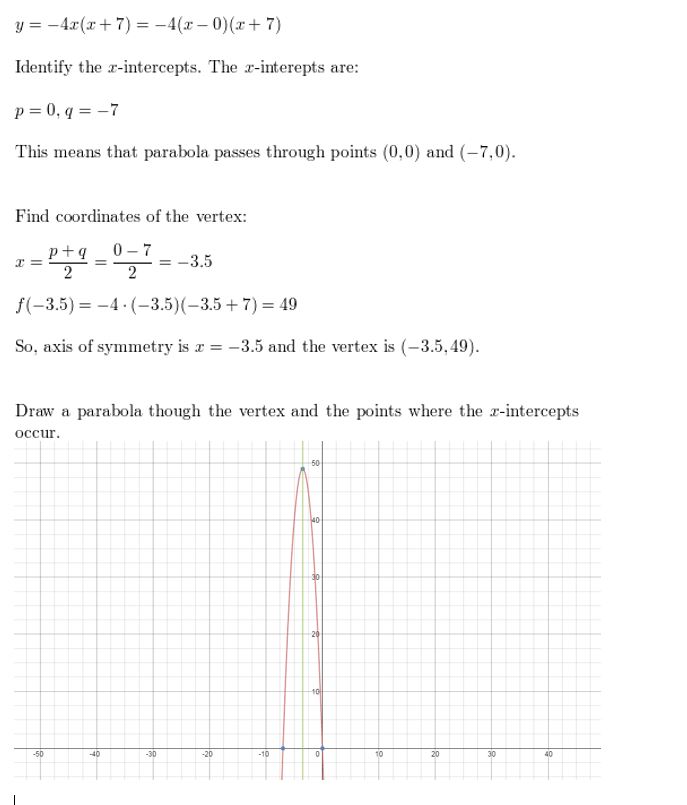
Question 59.
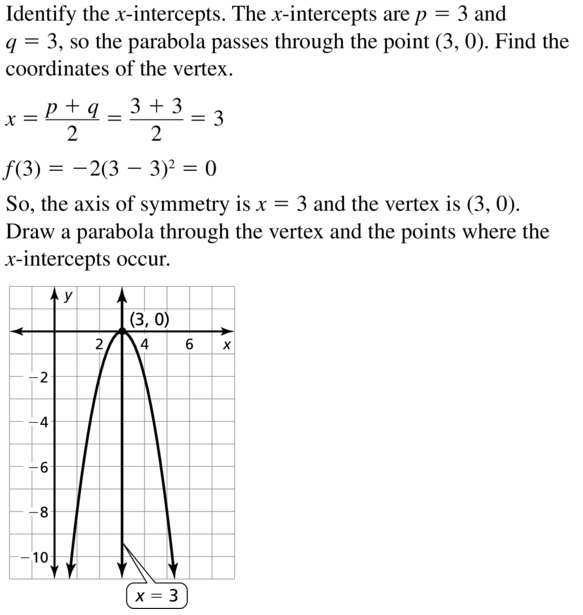
f(x) = -ii(x – 3)²
Respond:

Question 60.
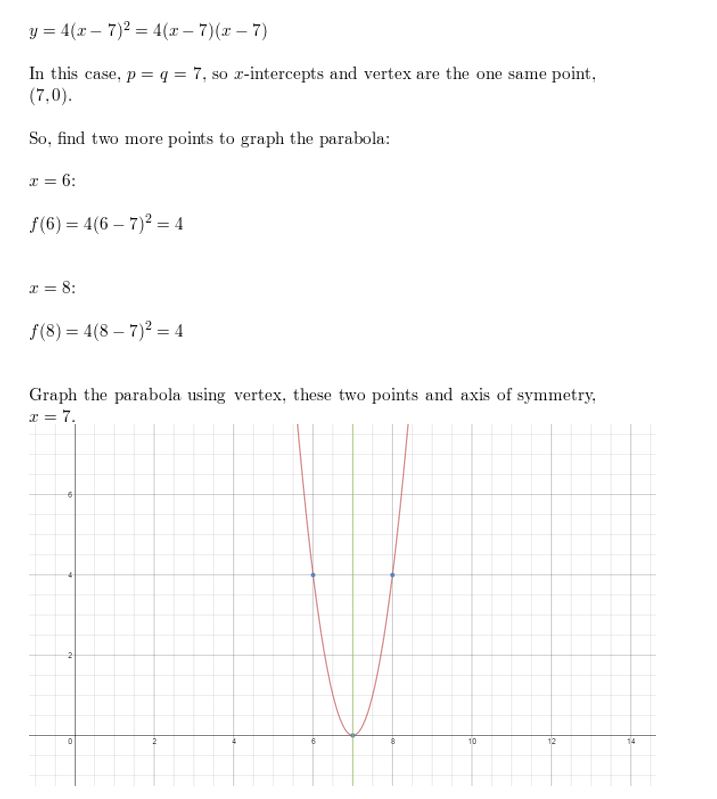
y = 4(ten – 7)²
Answer:

USING TOOLS In Exercises 61–64, place the ten-intercepts of the function and describe where the graph is increasing and decreasing. Utilize a graphing estimator to verify your answer.

Question 61.
f(x) = \(\frac{1}{2}\)(x – two)(10 + half dozen)
Respond:

Question 62.
y = \(\frac{3}{4}\)(x + 1)(10 – 3)
Answer:

Question 63.
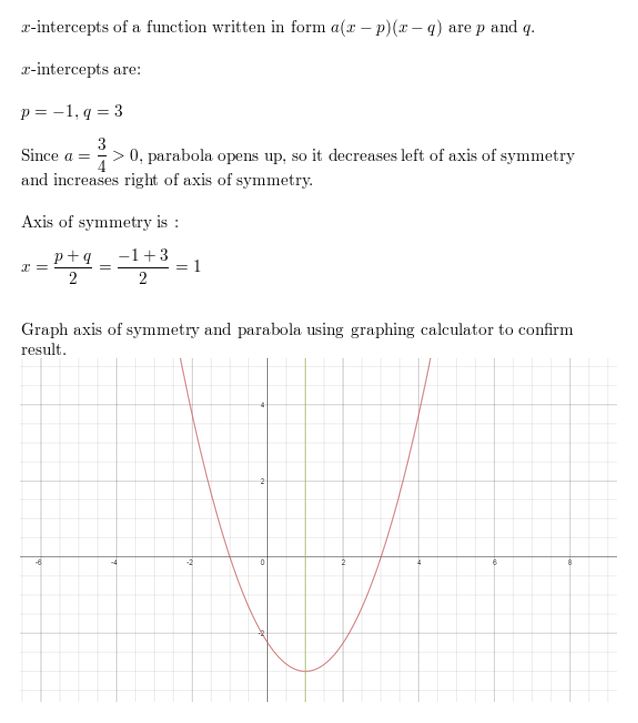
grand(10) = -four(x – 4)(x – 2)
Answer:

Question 64.
h(x) = -five(x + 5)(x + one)
Respond:

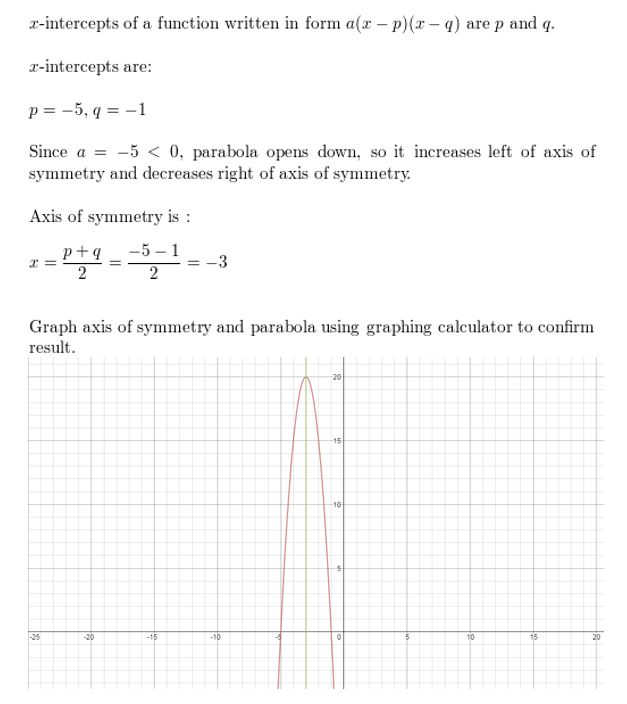
Question 65.
MODELING WITH MATHEMATICS A soccer player kicks a ball downfield. The height of the ball increases until it reaches a maximum peak of viii yards, 20 yards abroad from the actor. A second kick is modeled by y = x(0.4 – 0.008x). Which kick travels farther before hit the ground? Which kicking travels higher?

Answer:

Question 66.
MODELING WITH MATHEMATICS Although a football field appears to be flat, some are actually shaped similar a parabola then that rain runs off to both sides. The cross department of a field tin can be modeled by y = -0.000234x(10 – 160), where 10 and y are measured in feet. What is the width of the field? What is the maximum height of the surface of the field?

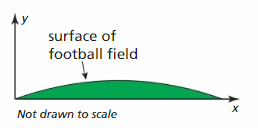
Reply:

Question 67.
REASONING The points (2, three) and (-4, ii) lie on the graph of a quadratic role. Determine whether you can apply these points to find the centrality of symmetry. If non, explain. If so, write the equation of the centrality of symmetry.
Answer:

Question 68.
Open up-Ended Write 2 different quadratic functions in intercept grade whose graphs take the centrality of symmetry x= 3.
Answer:

Question 69.
PROBLEM SOLVING An online music shop sells nearly 4000 songs each day when it charges $i per song. For each $0.05 increment in price, about 80 fewer songs per day are sold. Use the verbal model and quadratic function to determine how much the store should charge per song to maximize daily revenue.

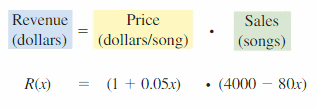
Answer:

Question 70.
PROBLEM SOLVING An electronics store sells lxx digital cameras per month at a price of $320 each. For each $xx decrease in cost, about v more cameras per month are sold. Employ the exact model and quadratic part to make up one's mind how much the store should accuse per camera to maximize monthly revenue.

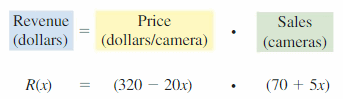
Reply:

Question 71.
Drawing CONCLUSIONS Compare the graphs of the three quadratic functions. What exercise you lot find? Rewrite the functions f and g in standard form to justify your answer.
f(x) = (x + 3)(x + ane)
g(x) = (x + 2)² – 1
h(ten) = 10² + 4x + 3
Answer:

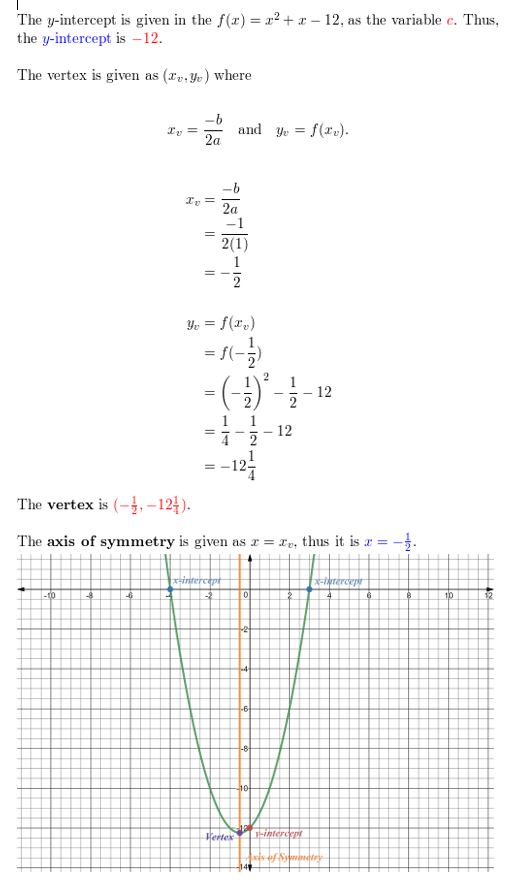
Question 72.
USING STRUCTURE Write the quadratic part f(x) = xⁱⁱ + ten – 12 in intercept form. Graph the function. Label the 10-intercepts, y-intercept, vertex, and axis of symmetry.
Answer:

Question 73.
Trouble SOLVING A woodland jumping mouse hops along a parabolic path given past y = -0.2xⁱⁱ + ane.3x, where x is the mouse'southward horizontal distance traveled (in anxiety) and y is the corresponding height (in feet). Tin can the mouse jump over a fence that is iii feet high? Justify your answer.

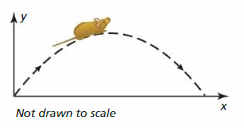
Answer:

Question 74.
HOW Exercise You Encounter It? Consider the graph of the function f(10) = a(ten – p)(ten – q).

a. What does f(\(\frac{p+q}{2}\)) correspond in the graph?
b. If a < 0, how does your answer in part (a) change? Explain.
Answer:

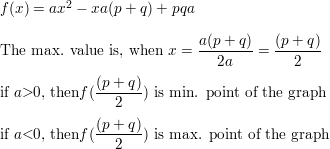
Question 75.
MODELING WITH MATHEMATICS The Gateshead Millennium Bridge spans the River Tyne. The curvation of the span can be modeled by a parabola. The arch reaches a maximum height of 50 meters at a betoken roughly 63 meters beyond the river. Graph the bend of the arch. What are the domain and range? What do they stand for in this situation?

Answer:

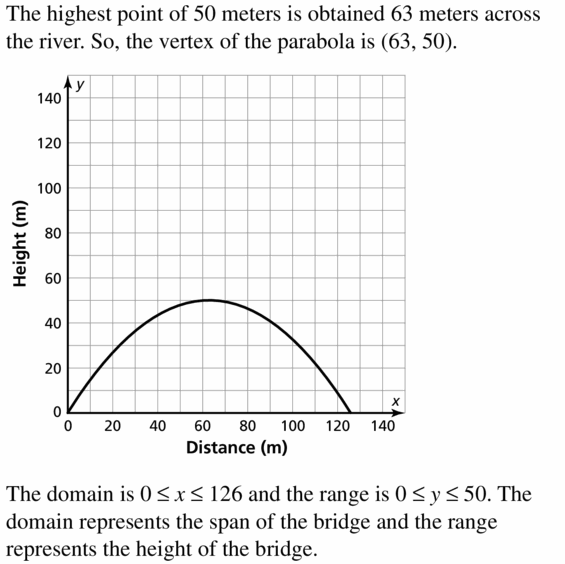
Quadratic 76.
Idea PROVOKING
Yous have 100 anxiety of fencing to enclose a rectangular garden. Draw three possible designs for the garden. Of these, which has the greatest area? Make a conjecture about the dimensions of the rectangular garden with the greatest possible area. Explain your reasoning.
Respond:

Question 77.
MAKING AN Argument The point (1, five) lies on the graph of a quadratic part with centrality of symmetry x = -1. Your friend says the vertex could exist the point (0, 5). Is your friend correct? Explain.
Reply:

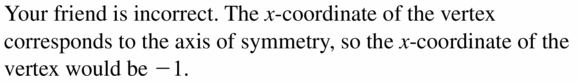
Question 78.
Disquisitional THINKING Observe the y-intercept in terms of a, p, and q for the quadratic function f(x) = a(x – p)(x – q).
Answer:

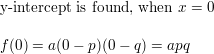
Question 79.
MODELING WITH MATHEMATICS A kernel of popcorn contains water that expands when the kernel is heated, causing it to pop. The equations beneath represent the "popping volume" y (in cubic centimeters per gram) of popcorn with moisture content ten (as a percent of the popcorn's weight).
Hot-air popping: y = -0.761(ten – 5.52)(x – 22.6)
Hot-oil popping:y = -0.652(x – 5.35)(x – 21.eight)

a. For hot-air popping, what wet content maximizes popping volume? What is the maximum book?
b. For hot-oil popping, what moisture content maximizes popping volume? What is the maximum book?
c. Employ a graphing calculator to graph both functions in the same coordinate airplane. What are the domain and range of each function in this situation? Explain.
Respond:

Question 80.
ABSTRACT REASONING A role is written in intercept form with a > 0. What happens to the vertex of the graph as a increases? as a approaches 0?
Respond:

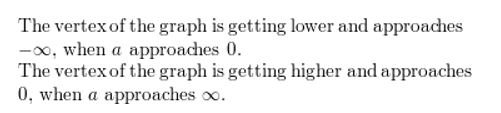
Maintaining Mathematical Proficiency

Solve the equation. Check for extraneous solutions. (Skills Review Handbook)

Question 81.
3\(\sqrt{x}\) – half-dozen = 0
Reply:

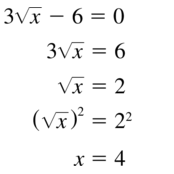
Question 82.
two\(\sqrt{ten-4}\) – ii = 2
Respond:

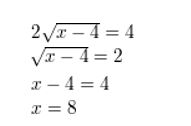
Question 83.
\(\sqrt{5x}\) + 5 = 0
Answer:

Question 84.
\(\sqrt{3x+8}\) = \(\sqrt{x+4}\)
Answer:

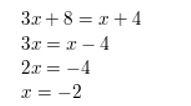
Solve the proportion. (Skills Review Handbook)

Question 85.
\(\frac{one}{2}\) = \(\frac{10}{4}\)
Answer:

Question 86.
\(\frac{2}{3}\) = \(\frac{ten}{9}\)
Answer:

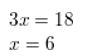
Question 87.
\(\frac{-ane}{4}\) = \(\frac{3}{10}\)
Answer:

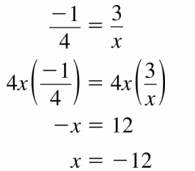
Question 88.
\(\frac{5}{ii}\) =-\(\frac{20}{x}\)
Reply:

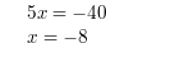
Quadratic Functions Study Skills Using the Features of Your Textbook to Prepare for Quizzes and Tests

Core Vocabulary

Cadre Concepts

Section ii.one

Section 2.two

Mathematical Practices

Question ane.
Why does the summit you found in Exercise 44 on folio 53 make sense in the context of the situation?

Question 2.
How tin you effectively communicate your preference in methods to others in Exercise 47 on folio 54?

Question 3.
How can yous utilise technology to deepen your agreement of the concepts in Exercise 79 on page 64?

Study Skills
Using the Features of Your Textbook to Prepare for Quizzes and Tests

• Read and understand the core vocabulary and the contents of the Core Concept boxes.
• Review the Examples and the Monitoring Progress questions. Use the tutorials at BigIdeasMath.com for additional help.
• Review previously completed homework assignments.

Quadratic Functions ii.1 – two.2 Quiz

2.ane – 2.ii Quiz

Draw the transformation of f(x) = 10ⁱⁱ represented by g. (Section 2.1)

Question 1.

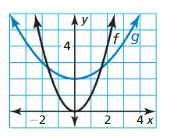
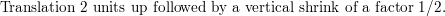
Question 2.

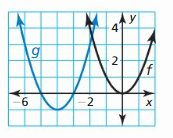
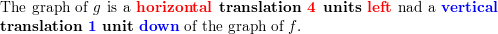
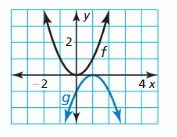
Question 3.

Write a rule for one thousand and identify the vertex. (Section ii.one)

Question four.
Let g be a translation 2 units up followed by a reflection in the ten-axis and a vertical stretch by a cistron of half-dozen of the graph of f(x) = x².

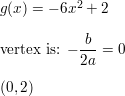
Question 5.
Let g be a translation 1 unit left and 6 units down, followed past a vertical shrink by a factor of \(\frac{1}{2}\) of the graph of f(x) = 3(x + 2)².

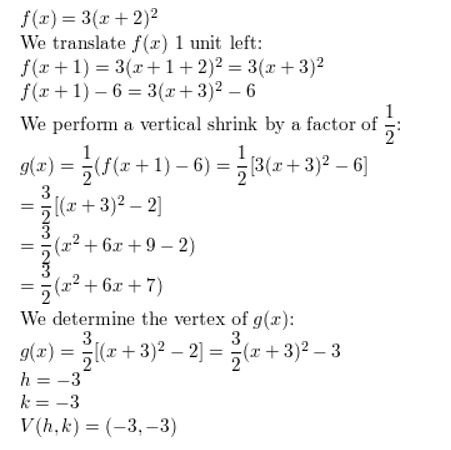
Question six.
Permit g be a horizontal compress by a cistron of \(\frac{1}{iv}\), followed by a translation 1 unit of measurement up and three units right of the graph of f(x) = (2x + ane)² – 11.

Graph the function. Label the vertex and centrality of symmetry. (Department 2.2)

Question 7.
f(x) = 2(ten – 1)² – 5

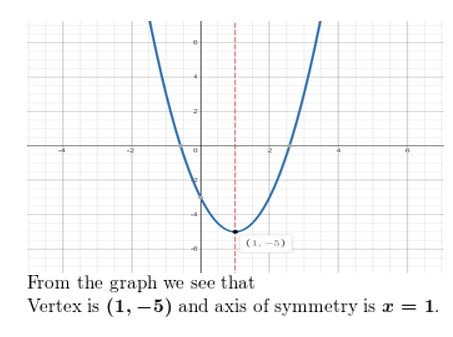
Question viii.
h(ten) = 3x² + 6x – 2

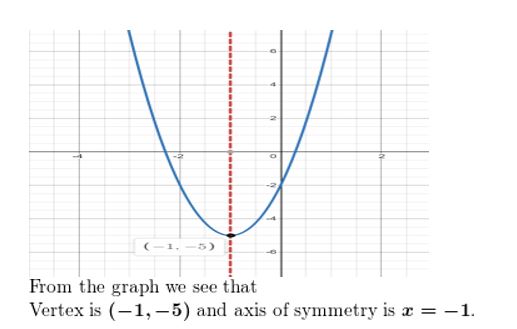
Question 9.
f(10) = 7 – 8x – 10²

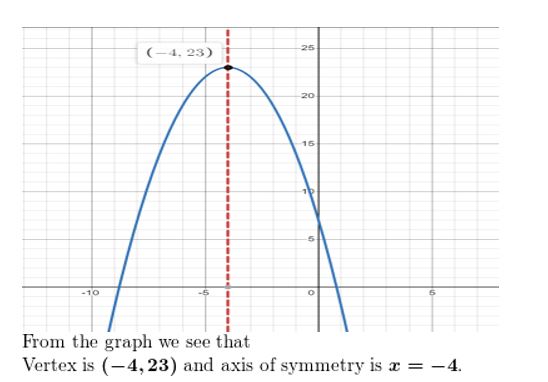
Find the 10-intercepts of the graph of the function. Then draw where the function is increasing and decreasing.(Department 2.2)

Question 10.
one thousand(10) = -iii(x + 2)(x + 4)

Question xi.
g(x) = \(\frac{i}{2}\)(ten – v)(x + ane)

Question 12.
f(x) = 0.4x(10 – 6)

Question 13.
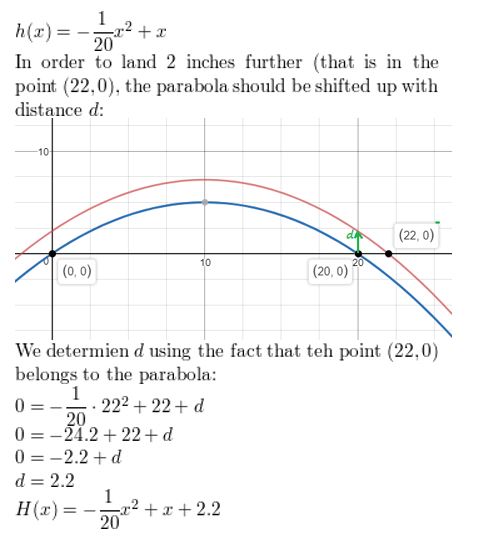
A grasshopper can leap incredible distances, up to 20 times its length. The height (in inches) of the spring above the ground of a 1-inch-long grasshopper is given by h(x) = –\(\frac{1}{xx}\)10² + x, where x is the horizontal altitude (in inches) of the bound. When the grasshopper jumps off a rock, information technology lands on the basis 2 inches farther. Write a part that models the new path of the jump. (Section 2.ane)

Question 14.
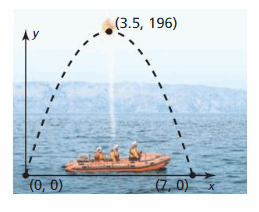
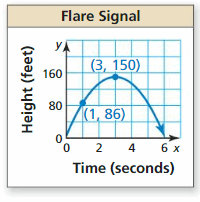
A passenger on a stranded lifeboat shoots a distress flare into the air. The height (in feet) of the flare above the h2o is given by f(t) = -16t(t – viii), where t is time (in seconds) since the flare was shot. The rider shoots a 2d flare, whose path is modeled in the graph. Which flare travels higher? Which remains in the air longer? Justify your answer. (Section ii.ii)

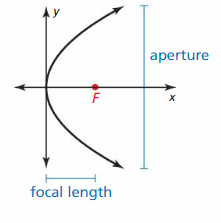
Lesson 2.3 Focus of a Parabola

Essential Question
What is the focus of a parabola?
EXPLORATION 1
Analyzing Satellite Dishes
Work with a partner. Vertical rays enter a satellite dish whose cantankerous section is a parabola. When the rays hitting the parabola, they reverberate at the same angle at which they entered. (See Ray ane in the figure.)
a. Describe the reflected rays then that they intersect the y-centrality.
b. What do the reflected rays take in mutual?
c. The optimal location for the receiver of the satellite dish is at a point chosen the focus of the parabola. Determine the location of the focus. Explicate why this makes sense in this situation.

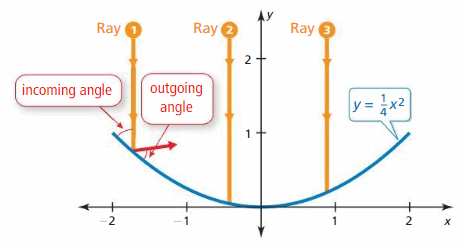
EXPLORATION two
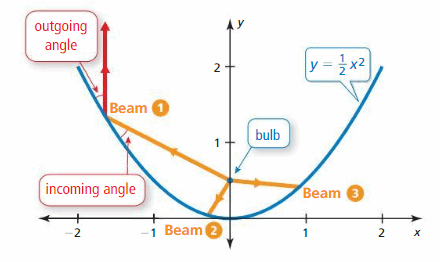
Analyzing Spotlights

Work with a partner. Beams of light are coming from the bulb in a spotlight, located at the focus of the parabola. When the beams hit the parabola, they reflect at the aforementioned angle at which they hitting. (See Axle 1 in the effigy.) Draw the reflected beams. What do they have in common? Would you consider this to exist the optimal result? Explain.

Communicate Your Respond

Question 3.
What is the focus of a parabola?
A parabola is set up of all points in a plane which are an equal distance away from a given point and given line.

Question iv.
Draw some of the properties of the focus of a parabola.
Thefocus does not prevarication on the directrix. Theparabola is the locus of points in that plane that are equidistant from both the directrix and thefocus.

2.3 Lesson

Monitoring Progress

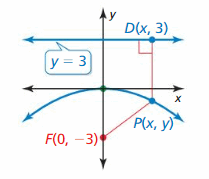
Question 1.
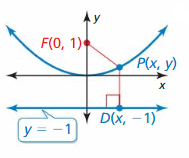
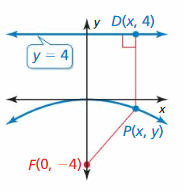
Use the Distance Formula to write an equation of the parabola with focus F(0, -3) and directrix y = three.

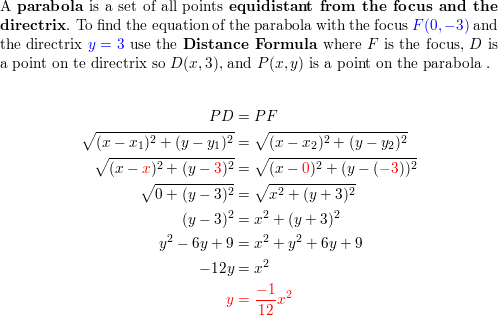
Place the focus, directrix, and axis of symmetry of the parabola. Then graph the equation.

Question two.
y = 0.5x²

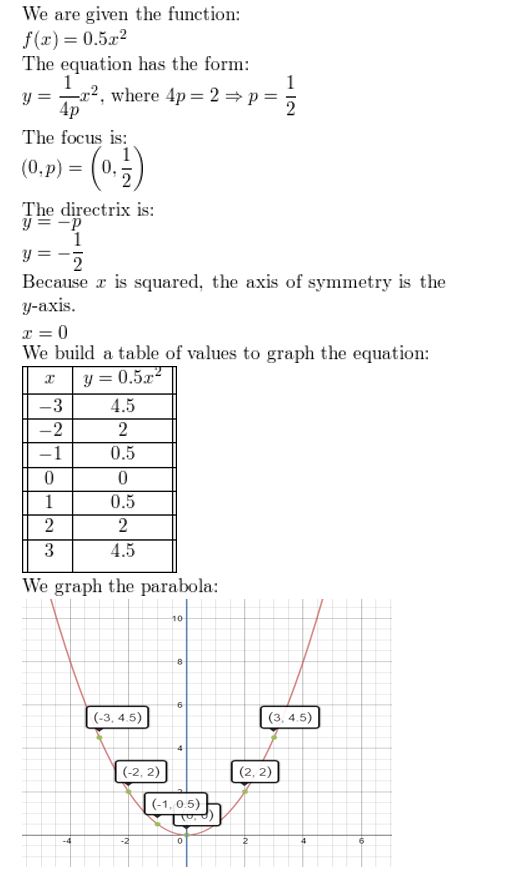
Question 3.
-y = x²

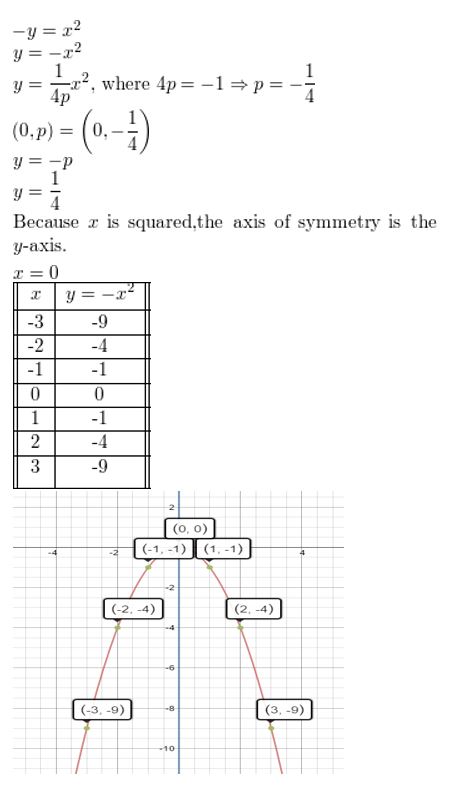
Question four.
y² = 6x

Write an equation of the parabola with vertex at (0, 0) and the given directrix or focus.

Question 5.
directrix: x = -3

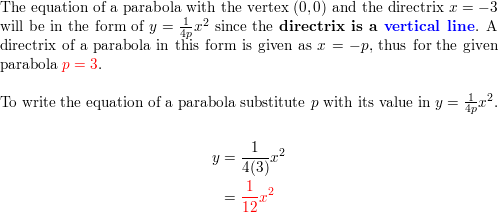
Question 6.
focus: (-2, 0)

Question seven.
focus: (0, \(\frac{3}{2}\))

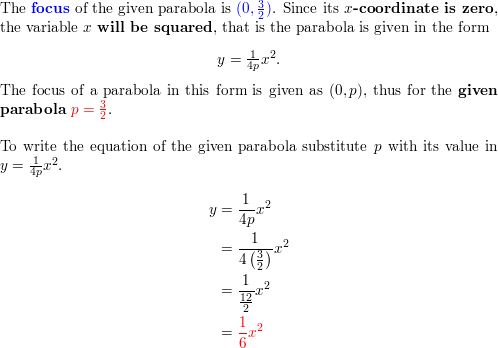
Monitoring Progress

Question eight.
Write an equation of a parabola with vertex (-1, 4) and focus (-ane, 2).

Question 9.
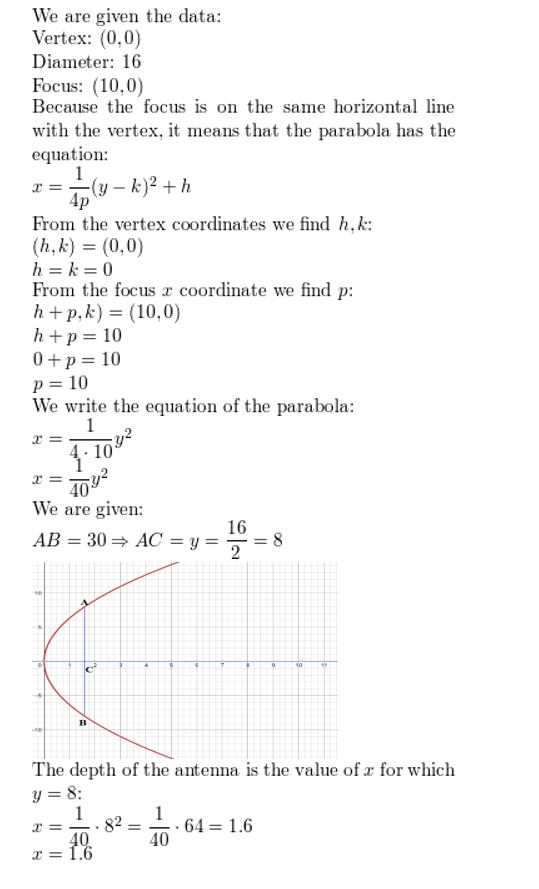
A parabolic microwave antenna is 16 feet in diameter. Write an equation that represents the cross section of the antenna with its vertex at (0, 0) and its focus 10 feet to the right of the vertex. What is the depth of the antenna?

Focus of a Parabola ii.3 Exercises

Vocabulary and Core Concept Check

Question 1.
Consummate THE SENTENCE A parabola is the set of all points in a plane equidistant from a stock-still betoken called the ______ and a fixed line called the __________ .
Respond:

Question 2.
WRITING Explain how to discover the coordinates of the focus of a parabola with vertex (0, 0)and directrix y = five.
Reply:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–x, use the Distance Formula to write an equation of the parabola.

Question 3.

Answer:

Question 4.

Answer:

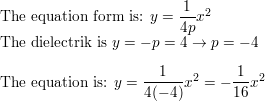
Question v.
focus: (0, -2)
directrix: y = ii
Answer:

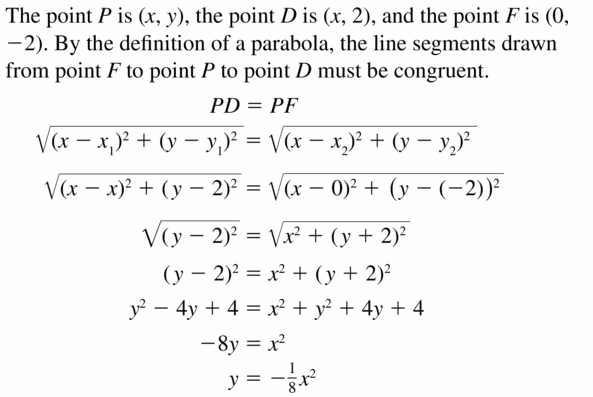
Question 6.
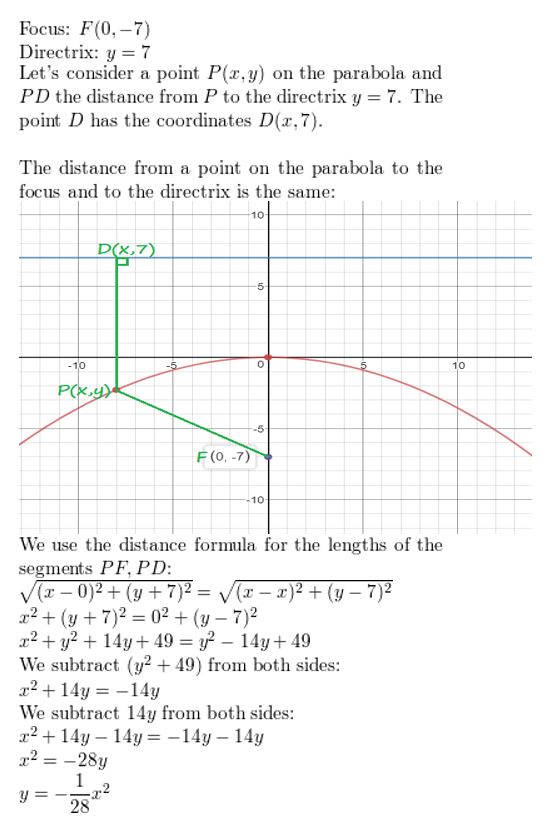
directrix: y = vii
focus: (0, -seven)
Answer:

Question 7.
vertex: (0, 0)
directrix: y = -6
Answer:

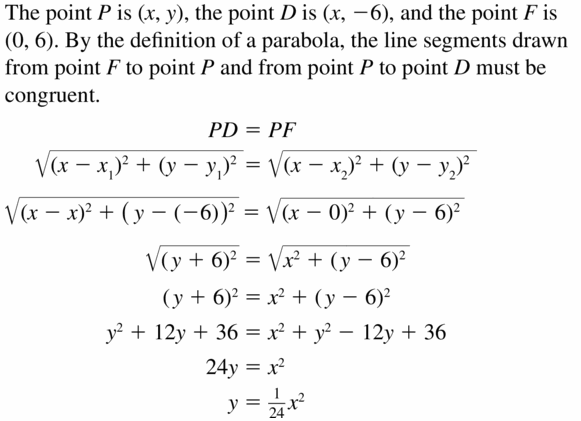
Question 8.
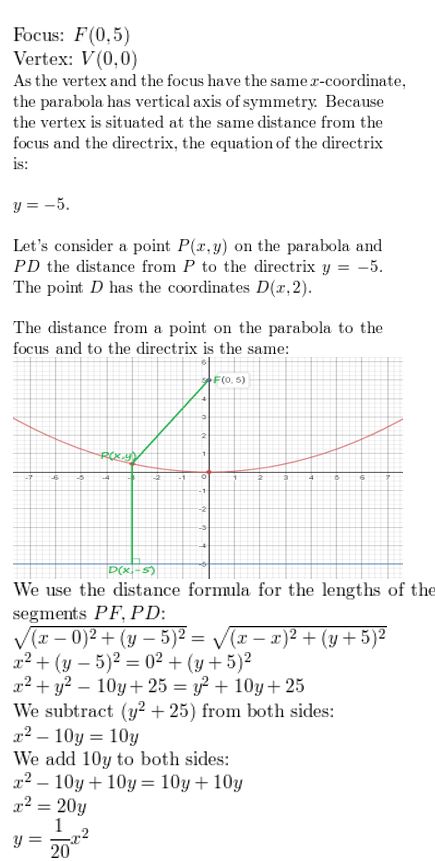
vertex: (0, 0)
focus: (0, five)
Answer:

Question 9.
vertex: (0, 0)
focus: (0, -10)
Answer:

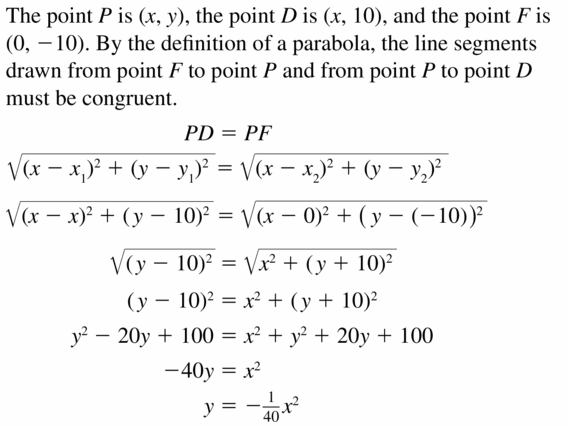
Question 10.
vertex: (0, 0)
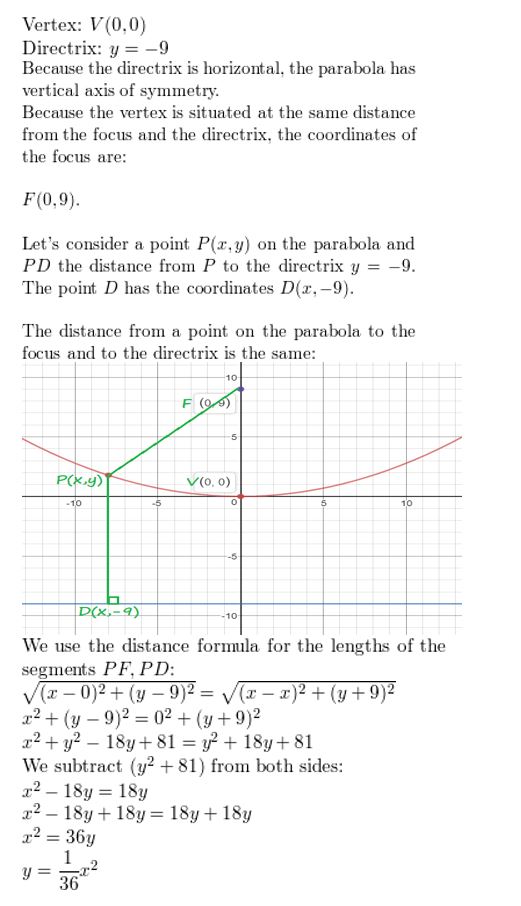
directrix: y = -9
Answer:

Question 11.
ANALYZING RELATIONSHIPS Which of the given characteristics describe parabolas that open up down? Explain your reasoning.
A. focus: (0, -6)
directrix: y = 6
B. focus: (0, -2)
directrix: y = 2
C.focus: (0, 6)
directrix: y = -vi
D. focus: (0, -1)
directrix: y = ane
Answer:

Question 12.
REASONING Which of the following are possible coordinates of the point P in the graph shown? Explicate.

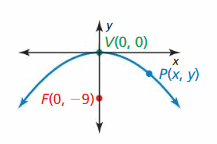
A. (-6, -1)
B. (3, –\(\frac{1}{4}\))
C. (4, –\(\frac{4}{9}\))
D. (ane, –\(\frac{1}{36}\))
Due east. (6, -1)
F. (two, –\(\frac{one}{eighteen}\))
Reply:

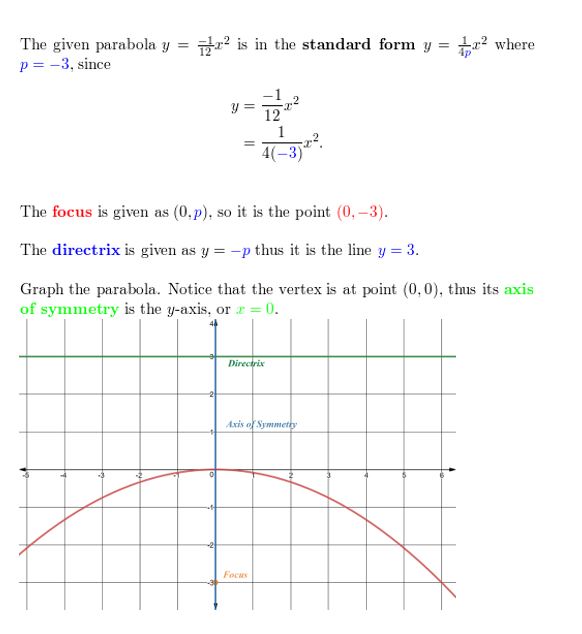
In Exercises thirteen–xx, identify the focus, directrix, and axis of symmetry of the parabola. Graph the equation.

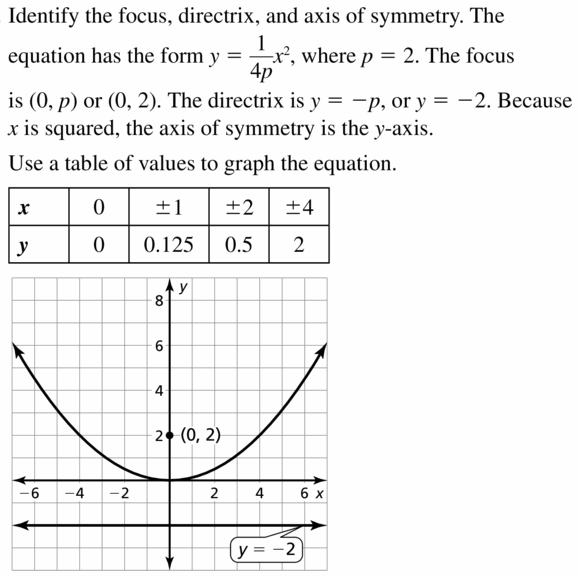
Question 13.
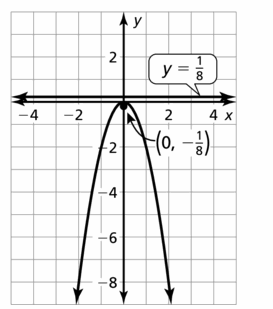
y = \(\frac{i}{8}\)10²
Answer:

Question 14.
y = –\(\frac{1}{12}\)x^two
Answer:

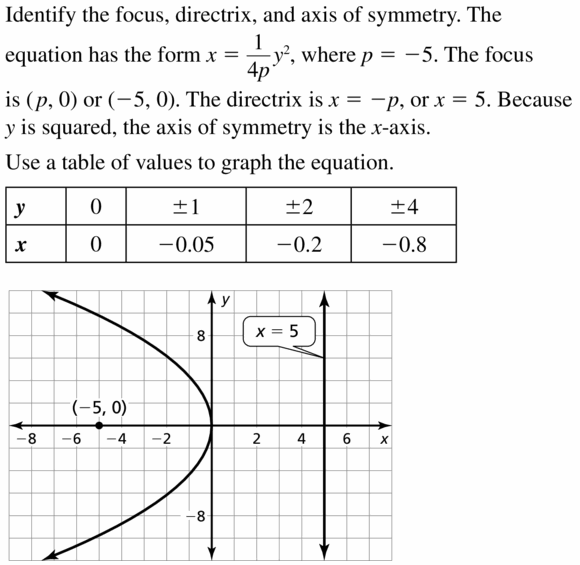
Question 15.
10 = –\(\frac{ane}{xx}\)y²
Respond:

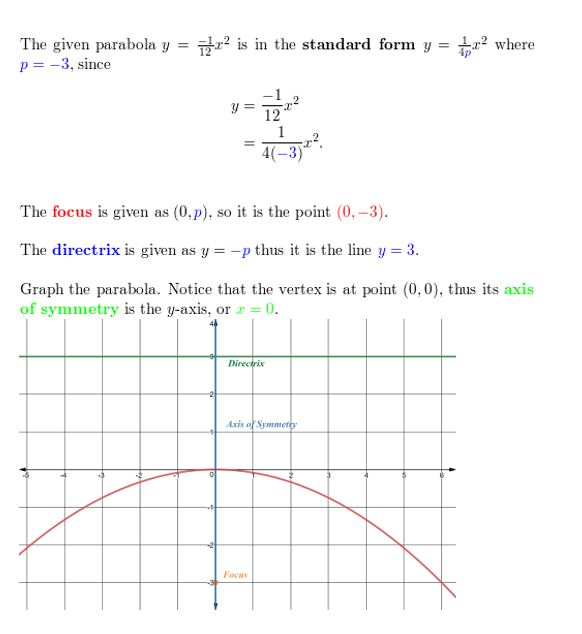
Question xvi.
x= \(\frac{ane}{24}\)y^two
Answer:

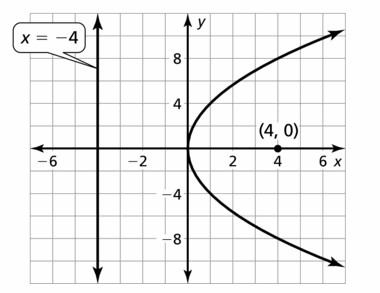
Question 17.
y² = 16x
Answer:

Question 18.
-xⁱⁱ = 48y
Answer:

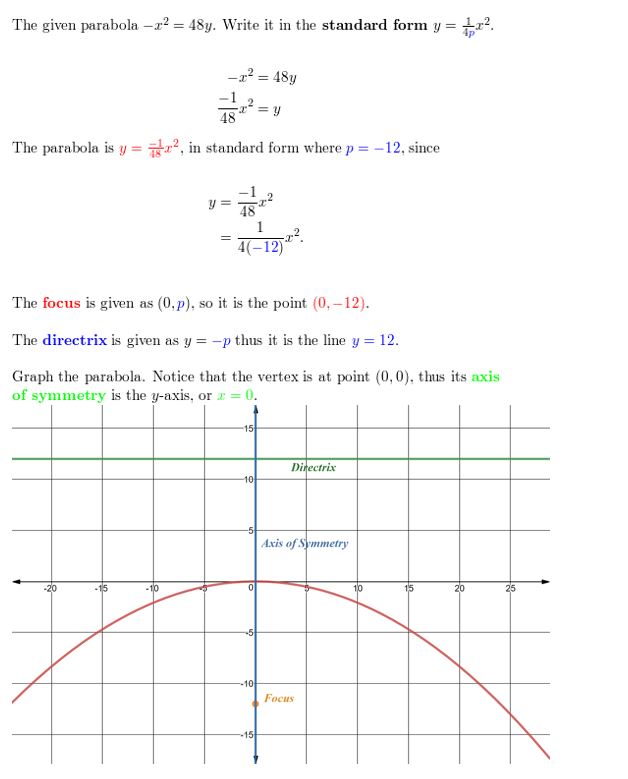
Question nineteen.
6x² + 3y = 0
Answer:

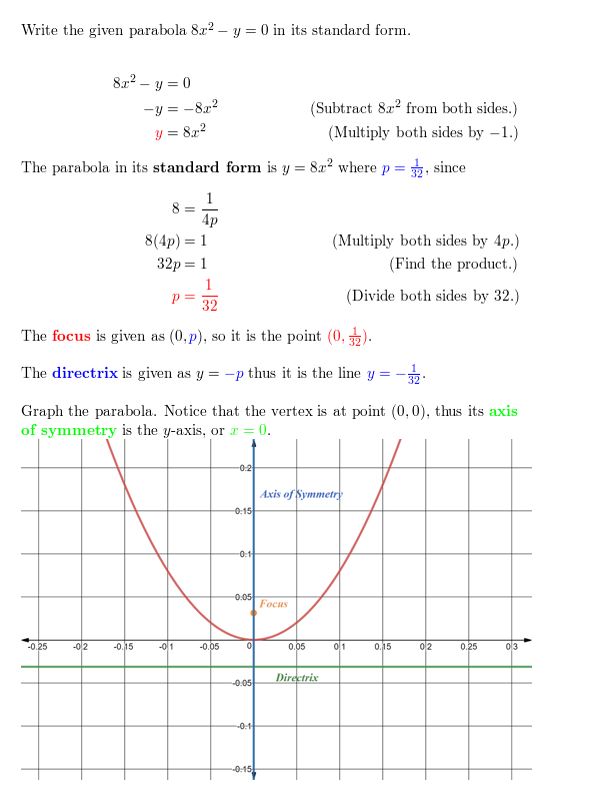
Question xx.
8x² – y = 0
Answer:

Fault Assay In Exercises 21 and 22, depict and correct the fault in graphing the parabola.

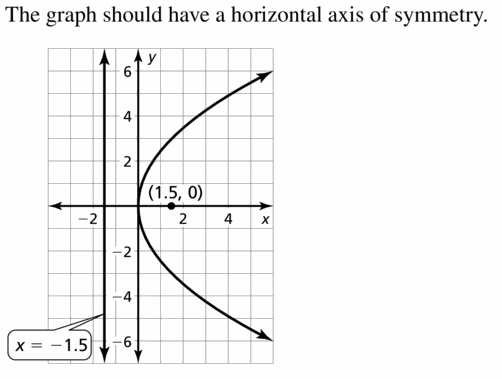
Question 21.

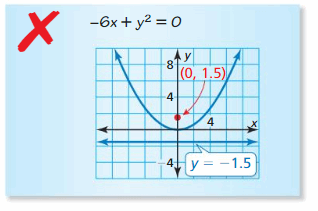
Answer:

Question 22.

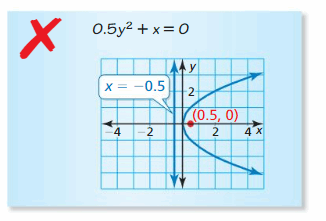
Reply:

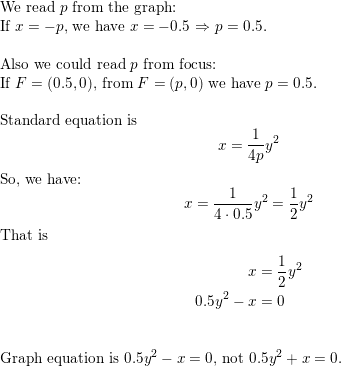
Question 23.
ANALYZING EQUATIONS The cantankerous section (with units in inches) of a parabolic satellite dish can be modeled by the equation y = \(\frac{1}{38}\)x². How far is the receiver from the vertex of the cross section? Explicate.
Respond:

Question 24.
ANALYZING EQUATIONS The cantankerous section (with units in inches) of a parabolic spotlight can be modeled by the equation x = \(\frac{i}{20}\)y^two. How far is the bulb from the vertex of the cross section? Explicate.

Answer:

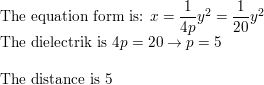
In Exercises 25–28, write an equation of the parabola shown.

Question 25.

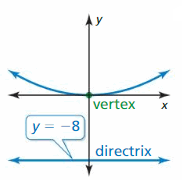
Answer:

Question 26.

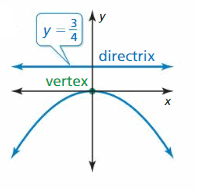
Reply:

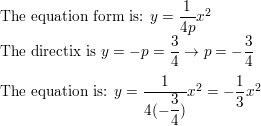
Question 27.

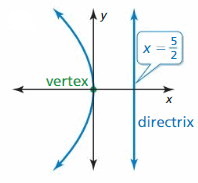
Answer:

Question 28.

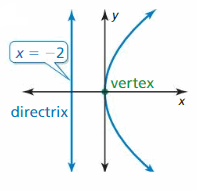
Answer:

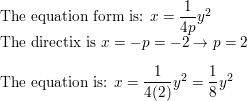
In Exercises 29–36, write an equation of the parabola with the given characteristics.

Question 29.
focus: (3, 0)
directrix: x = -3
Answer:

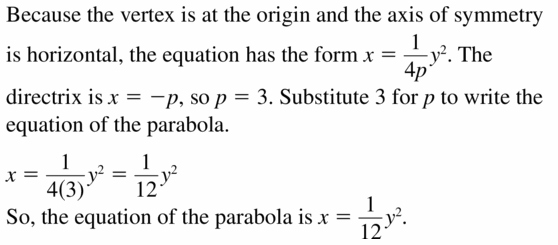
Questio
thirty.
focus: (\(\frac{2}{3}\), 0)
directrix: x = –\(\frac{two}{3}\)
Reply:

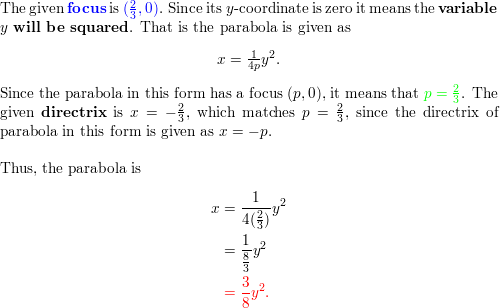
Question 31.
directrix: ten = -10
vertex: (0, 0)
Respond:

Question 32.
directrix: y = \(\frac{8}{iii}\)
vertex: (0, 0)
Respond:

Question 33.
focus: (0, –\(\frac{5}{three}\))
directrix: y = \(\frac{5}{iii}\)
Respond:

Question 34.
focus: (0, \(\frac{5}{iv}\))
directrix: y = –\(\frac{v}{four}\)
Answer:

Question 35.
focus: (0, \(\frac{6}{7}\))
vertex: (0, 0)
Answer:

Question 36.
focus: (-\(\frac{iv}{five}\), 0)
vertex: (0, 0)
Answer:

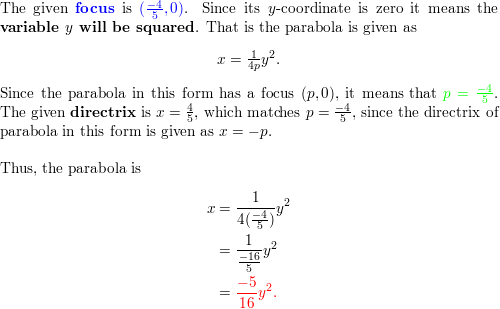
In Exercises 37–40, write an equation of the parabola shown.

Question 37.

Answer:

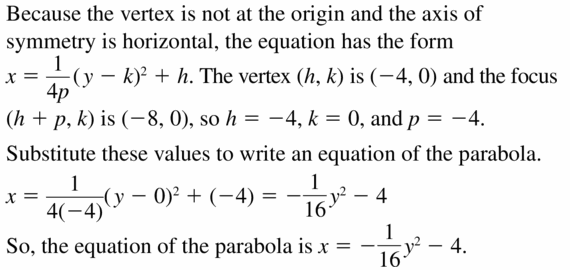
Question 38.

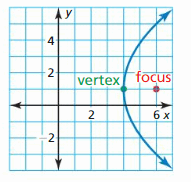
Respond:

Question 39.

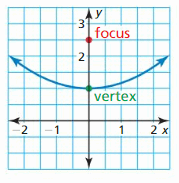
Answer:

Question 40.

Answer:

In Exercises 41–46, identify the vertex, focus, directrix, and axis of symmetry of the parabola. Describe the transformations of the graph of the standard equation with p = 1 and vertex (0, 0).

Question 41.
y = \(\frac{1}{8}\)(10 – 3)^two + 2
Answer:

Question 42.
y = –\(\frac{1}{4}\)(x + 2)² + 1
Answer:

Question 43.
ten = \(\frac{ane}{xvi}\)(y – iii)² + 1
Answer:

Question 44.
y = (x + three)² – five
Reply:

Question 45.
x = -3(y + 4)² + two
Reply:

Question 46.
10 = 4(y + 5)^two – 1
Answer:

Question 47.
MODELING WITH MATHEMATICS Scientists studying dolphin echolocation simulate the projection of a bottlenose dolphin'south clicking sounds using figurer models. The models originate the sounds at the focus of a parabolic reflector. The parabola in the graph shows the cross section of the reflector with focal length of 1.three inches and aperture width of viii inches. Write an equation to represent the cross section of the reflector. What is the depth of the reflector?

Answer:

Question 48.
MODELING WITH MATHEMATICS Solar energy can exist concentrated using long troughs that have a parabolic cross section as shown in the figure. Write an equation to represent the cross section of the trough. What are the domain and range in this situation? What practice they represent?

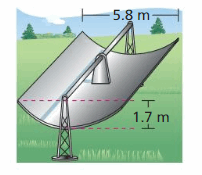
Answer:

Question 49.
ABSTRACT REASONING As | p | increases, how does the width of the graph of the equation y = \(\frac{ane}{iv p}\)10² change? Explain your reasoning.
Respond:

Question 50.
HOW DO You lot SEE IT? The graph shows the path of a volleyball served from an initial meridian of six feet every bit information technology travels over a internet.

a. Label the vertex, focus, and a point on the directrix.
b. An underhand serve follows the same parabolic path but is hit from a peak of three feet. How does this affect the focus? the directrix?
Answer:

Question 51.
CRITICAL THINKING The altitude from signal P to the directrix is ii units. Write an equation of the parabola.

Answer:

Question 52.
THOUGHT PROVOKING Two parabolas have the aforementioned focus (a, b) and focal length of 2 units. Write an equation of each parabola. Place the directrix of each parabola.
Respond:

Question 53.
REPEATED REASONING Utilise the Altitude Formula to derive the equation of a parabola that opens to the right with vertex (0, 0), focus (p, 0), and directrix ten = -p.

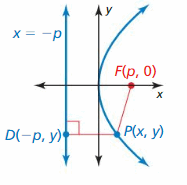
Answer:

Question 54.
PROBLEM SOLVING The latus rectum of a parabola is the line segment that is parallel to the directrix, passes through the focus, and has endpoints that lie on the parabola. Find the length of the latus rectum of the parabola shown.

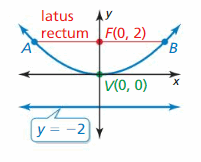
Reply:

Maintaining Mathematical Proficiency

Write an equation of the line that passes through the points.(Section 1.3)

Question 55.
(one, -iv), (two, -1)
Respond:

Question 56.
(-3, 12), (0, 6)
Reply:

Question 57.
(three, one), (-five, 5)
Answer:

Question 58.
(2, -one), (0, ane)
Answer:

Use a graphing calculator to find an equation for the line of all-time fit.

Question 59.

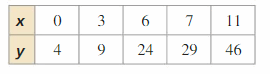
Answer:

Question 60.

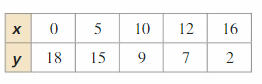
Answer:

Lesson 2.iv Modeling with Quadratic Functions

Essential Question
How tin can yous use a quadratic office to model a real-life state of affairs?

EXPLORATION 1
Modeling with a Quadratic Function

Work with a partner. The graph shows a quadratic part of the form
P(t) = atⁱⁱ + bt + c

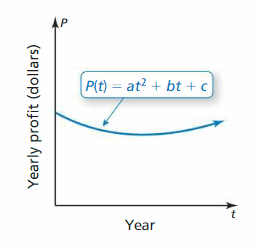
which approximates the yearly profits for a company, where P(t) is the turn a profit in yr t.
a. Is the value of a positive, negative, or zilch? Explicate.
b. Write an expression in terms of a and b that represents the yr t when the company made the least profit.
c. The visitor made the same yearly profits in 2004 and 2012. Estimate the yr in which the visitor made the least profit.
d. Assume that the model is still valid today. Are the yearly profits currently increasing, decreasing, or constant? Explain.

EXPLORATION ii
Modeling with a Graphing Calculator
Piece of work with a partner. The table shows the heights h (in anxiety) of a wrench t seconds after it has been dropped from a edifice nether construction.

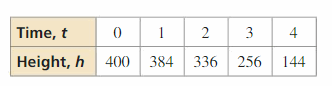
a. Use a graphing figurer to create a scatter plot of the information, equally shown at the right. Explain why the data appear to fit a quadratic model.
b. Utilize the quadratic regression feature to find a quadratic model for the data.
c. Graph the quadratic role on the same screen as the besprinkle plot to verify that information technology fits the data.


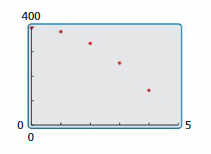
d. When does the wrench hit the basis? Explain.

Communicate Your Respond

Question three.
How can you lot use a quadratic function to model a real-life situation?

Question 4.
Use the Internet or some other reference to find examples of real-life situations that can be modeled past quadratic functions.
When you throw a brawl (or shoot an arrow, fire a missile or throw a stone) information technology goes up into the air, slowing equally information technology travels, so comes downward over again faster and faster .

2.4 Lesson

Monitoring Progress

Question 1.
WHAT IF? The vertex of the parabola is (50, 37.5). What is the top of the cyberspace?

Question 2.
Write an equation of the parabola that passes through the signal (-1, ii) and has vertex (4, -9).

Question 3.
WHAT IF? The y-intercept is 4.viii. How does this change your answers in parts (a) and (b)?

Question four.
Write an equation of the parabola that passes through the signal (ii, 5) and has x-intercepts -2 and 4.

Question five.
Write an equation of the parabola that passes through the points (-1, iv), (0, i), and (2, 7).

Question half dozen.
The table shows the estimated profits y (in dollars) for a concert when the charge is x dollars per ticket. Write and evaluate a role to determine what the charge per ticket should exist to maximize the profit.

Question 7.
The table shows the results of an experiment testing the maximum weights y (in tons) supported by ice 10 inches thick. Write a role that models the data. How much weight can be supported by ice that is 22 inches thick?

Modeling with Quadratic Functions 2.4 Exercises

Vocabulary and Core Concept Check

Question 1.
WRITING Explain when information technology is appropriate to employ a quadratic model for a set of data.
Answer:

Question 2.
Different WORDS, SAME QUESTION
Which is unlike? Observe "both" answers.

Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, write an equation of the parabola in vertex form.

Question 3.

Reply:

Question four.

Reply:

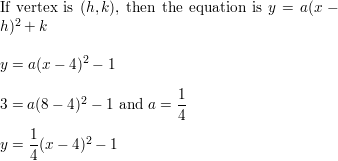
Question v.
passes through (13, 8) and has vertex (iii, 2)
Answer:

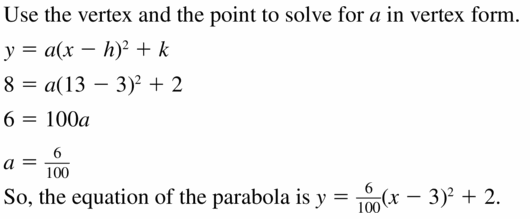
Question 6.
passes through (-7, -15) and has vertex (-5, ix)
Answer:

Question seven.
passes through (0, -24) and has vertex (-vi, -12)
Answer:

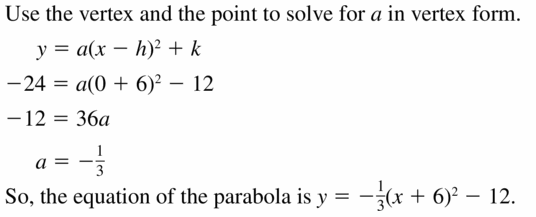
Question viii.
passes through (6, 35) and has vertex (-1, 14)
Answer:

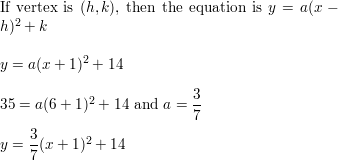
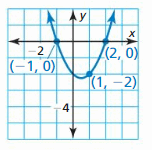
In Exercises nine–14, write an equation of the parabola in intercept course.

Question 9.

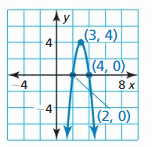
Answer:

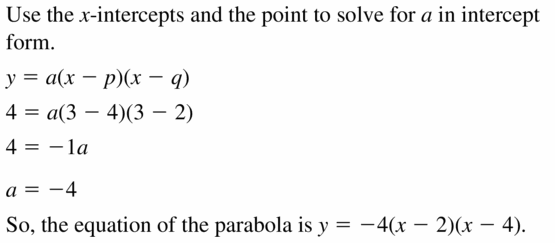
Question 10.

Reply:

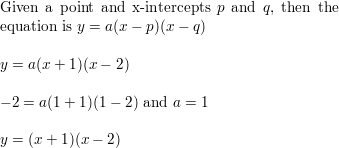
Question 11.
x-intercepts of 12 and -6; passes through (fourteen, four)
Reply:

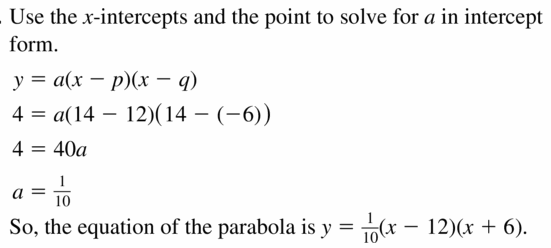
Question 12.
x-intercepts of 9 and i; passes through (0, -xviii)
Reply:

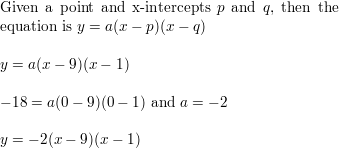
Question 13.
x-intercepts of -16 and -ii; passes through (-18, 72)
Respond:

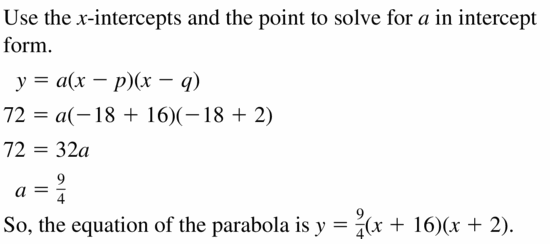
Question xiv.
x-intercepts of -seven and -3; passes through (-ii, 0.05)
Answer:

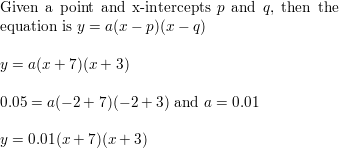
Question xv.
WRITING Explain when to use intercept form and when to use vertex form when writing an equation of a parabola.
Reply:

Question 16.
ANALYZING EQUATIONS Which of the following equations represent the parabola?

A. y = two(ten – 2)(10 + ane)
B. y = 2(x + 0.v)² – 4.v
C. y = 2(10 – 0.5)^two – 4.five
D. y = 2(ten + 2)(10 – 1)
Reply:

In Exercises 17–20, write an equation of the parabola in vertex form or intercept class.

Question 17.

Reply:

Question xviii.

Answer:

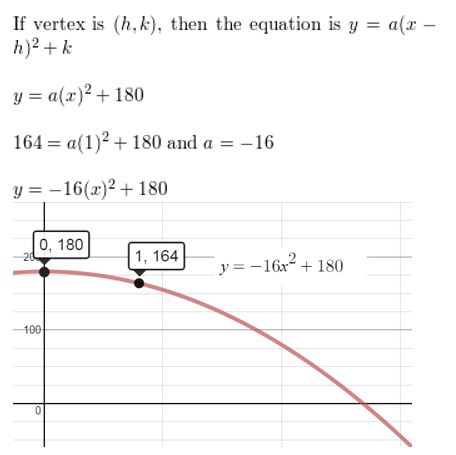
Question nineteen.

Answer:

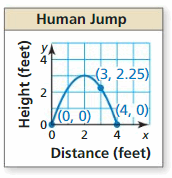
Question 20.

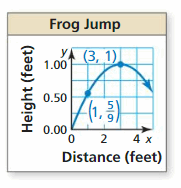
Answer:

Question 21.
Fault Assay Describe and correct the error in writing an equation of the parabola.

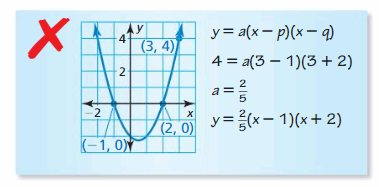
Respond:

Question 22.
MATHEMATICAL CONNECTIONS The area of a rectangle is modeled by the graph where y is the area (in foursquare meters) and x is the width (in meters). Write an equation of the parabola. Find the dimensions and corresponding expanse of 1 possible rectangle. What dimensions result in the maximum area?

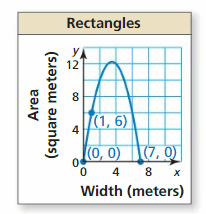
Answer:

Question 23.
MODELING WITH MATHEMATICS Every rope has a safe working load. A rope should not be used to lift a weight greater than its safe working load. The table shows the safe working loads S (in pounds) for ropes with circumference C (in inches). Write an equation for the condom working load for a rope. Discover the safe working load for a rope that has a circumference of x inches.

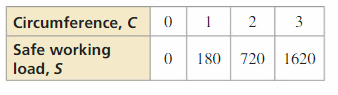
Answer:

Question 24.
MODELING WITH MATHEMATICS A baseball is thrown up in the air. The table shows the heights y (in feet) of the baseball later x seconds. Write an equation for the path of the baseball game. Find the superlative of the baseball after ane.7 seconds.

Respond:

Question 25.
Comparison METHODS You lot use a system with 3 variables to find the equation of a parabola that passes through the points (−8, 0), (two, −20), and (ane, 0). Your friend uses intercept form to find the equation. Whose method is easier? Justify your answer.
Answer:

Question 26.
MODELING WITH MATHEMATICS The table shows the distances y a motorcyclist is from home afterwards x hours.

a. Decide what type of office you tin use to model the data. Explain your reasoning.
b. Write and evaluate a role to determine the distance the motorcyclist is from home later 6 hours.
Answer:

Question 27.
USING TOOLS The tabular array shows the heights h (in feet) of a sponge t seconds later information technology was dropped by a window cleaner on elevation of a skyscraper.

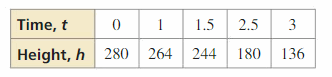
a. Use a graphing estimator to create a scatter plot. Which better represents the data, a line or a parabola? Explicate.
b. Utilize the regression feature of your calculator to find the model that best fits the data.
c. Employ the model in part (b) to predict when the sponge volition hit the ground.
d. Identify and interpret the domain and range in this state of affairs.
Answer:

Question 28.
MAKING AN Argument Your friend states that quadratic functions with the aforementioned x-intercepts have the same equations, vertex, and centrality of symmetry. Is your friend correct? Explain your reasoning.
Answer:

In Exercises 29–32, analyze the differences in the outputs to determine whether the data are linear, quadratic, or neither. Explain. If linear or quadratic, write an equation that fits the information.

Question 29.

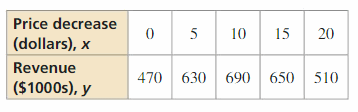
Answer:

Question thirty.

Answer:

Question 31.

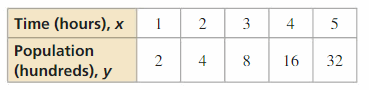
Answer:

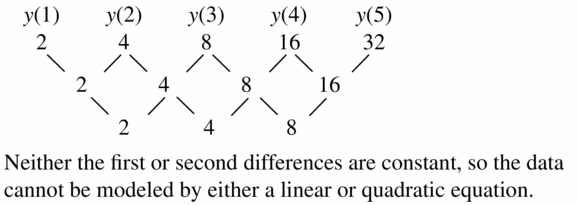
Question 32.

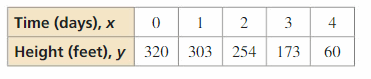
Answer:

Question 33.
Trouble SOLVING The graph shows the number y of students absent-minded from school due to the flu each day x.

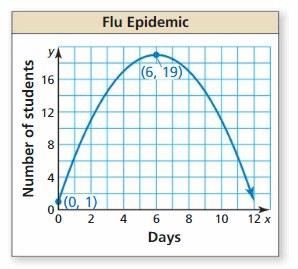
a. Interpret the meaning of the vertex in this situation.
b. Write an equation for the parabola to predict the number of students absent on 24-hour interval 10.
c. Compare the average rates of change in the students with the flu from 0 to six days and half dozen to eleven days.
Answer:

Question 34.
THOUGHT PROVOKING Describe a real-life state of affairs that tin exist modeled by a quadratic equation. Justify your answer.
Respond:

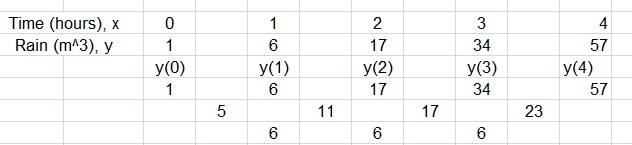
Question 35.
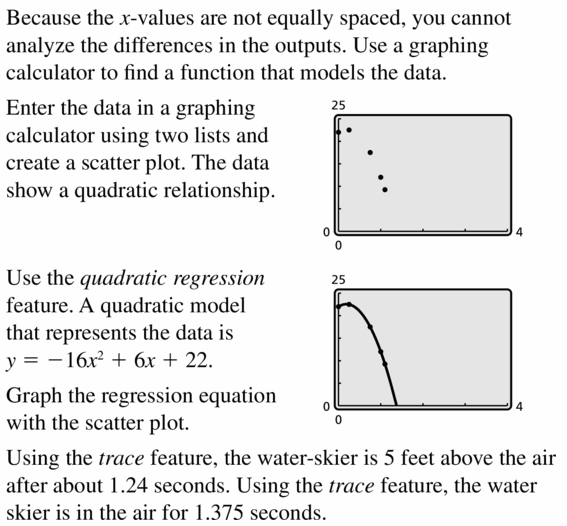
Problem SOLVING The tabular array shows the heights y of a competitive h2o-skier 10 seconds after jumping off a ramp. Write a office that models the elevation of the water-skier over time. When is the h2o-skier v feet higher up the water? How long is the skier in the air?

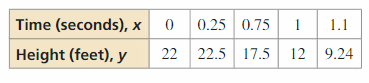
Reply:

Question 36.
HOW DO You lot See IT? Apply the graph to determine whether the average rate of change over each interval is positive, negative, or zero.

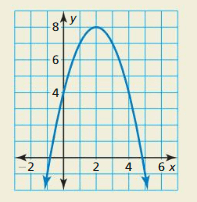
a. 0 ≤ x ≤ 2
b. 2 ≤ x ≤ 5
c. 2 ≤ 10 ≤ 4
d. 0 ≤ x ≤ 4
Answer:

Question 37.
REPEATED REASONING The tabular array shows the number of tiles in each figure. Verify that the data show a quadratic relationship. Predict the number of tiles in the twelfth figure.

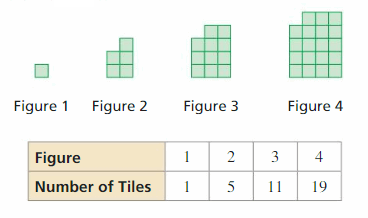
Respond:

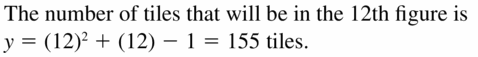
Maintaining Mathematical Proficiency

Factor the trinomial. (Skills Review Handbook)

Question 38.
x² + 4x + 3
Reply:

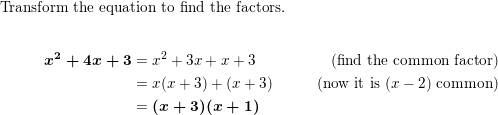
Question 39.
x² – 3x + ii
Reply:

Question 40.
3x² – 15x + 12
Reply:

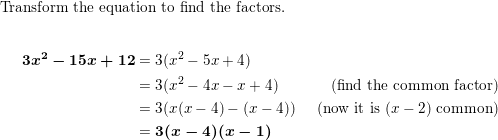
Question 41.
5x^two + 5x – 30
Respond:

Quadratic Functions Performance Chore: Accident Reconstruction

ii.3–2.4 What Did You Learn?

Core Vocabulary
focus, p. 68
directrix, p. 68

Core Concepts

Section 2.3
Standard Equations of a Parabola with Vertex at the Origin, p. 69
Standard Equations of a Parabola with Vertex at (h, k), p. 70

Section ii.iv
Writing Quadratic Equations, p. 76
Writing Quadratic Equations to Model Data, p. 78

Mathematical Practices

Question 1.
Explicate the solution pathway yous used to solve Practice 47 on page 73.

Question ii.
Explain how you used definitions to derive the equation in Exercise 53 on folio 74.

Question iii.
Explain the shortcut you institute to write the equation in Exercise 25 on page 81.

Question 4.
Describe how you were able to construct a feasible argument in Exercise 28 on page 81.

Operation Job

Accident Reconstruction

Was the driver of a motorcar speeding when the brakes were practical? What exercise skid marks at the scene of an blow reveal nigh the moments before the collision?

To explore the answers to these questions and more than, go to BigIdeasMath.com.

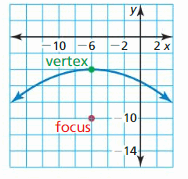
Quadratic Functions Chapter Review

Describe the transformation of f(x) = x² represented past g. Then graph each office.

Question one.
thou(x) = (x + four)^two

Question two.
g(x) = (ten – 7)^{2 + 2}

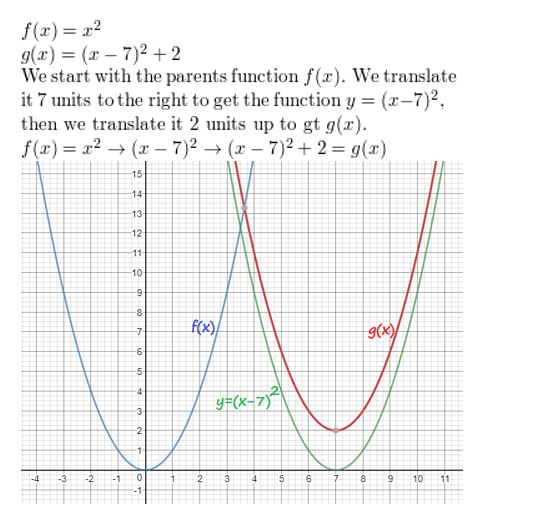
Question 3.
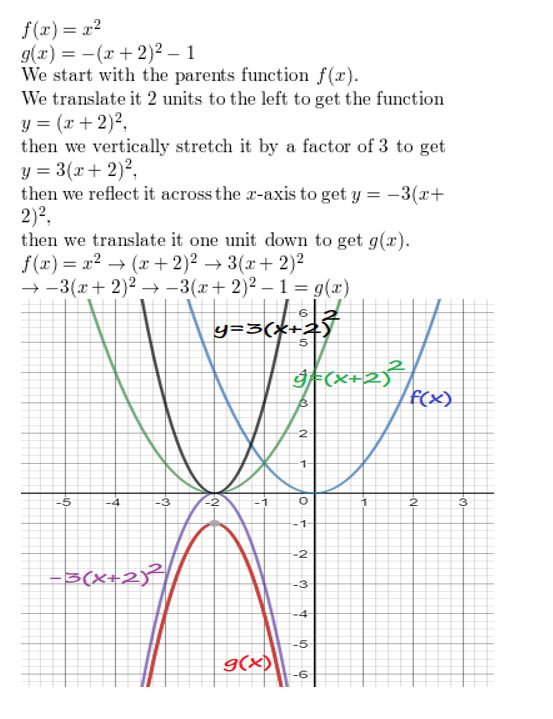
thousand(x) = -3(x + 2)² – 1

Question 4.
Let the graph of g be a horizontal shrink by a factor of \(\frac{2}{iii}\), followed by a translation five units left and 2 units downwardly of the graph of f(10) = ten².

Question 5.
Let the graph of g be a translation 2 units left and 3 units up, followed by a reflection in the y-axis of the graph of f(x) = x^two – 2x.

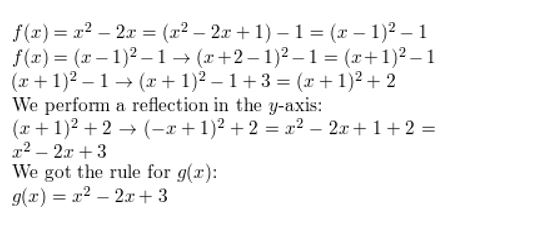
Graph the function. Label the vertex and centrality of symmetry. Find the minimum or maximum value of f. Describe where the function is increasing and decreasing.

Question 6.
f(x) = 3(x – 1)² – 4

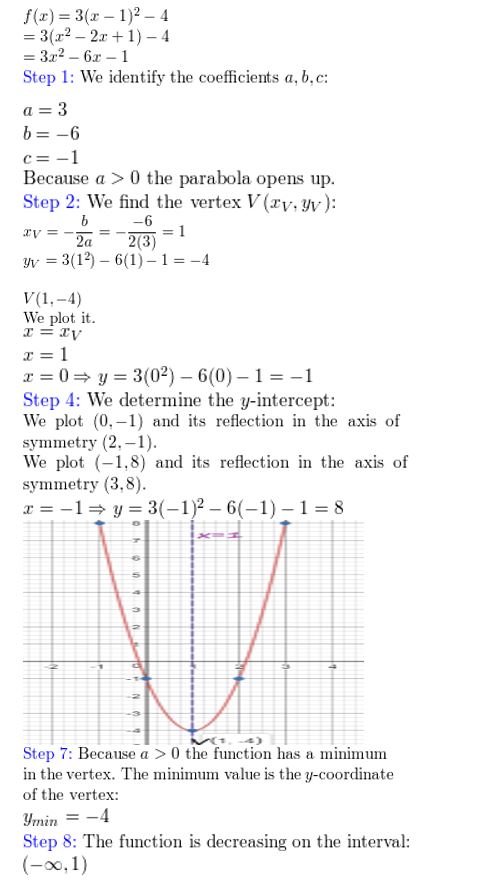
Question 7.
g(10) = -2x² + 16x + iii

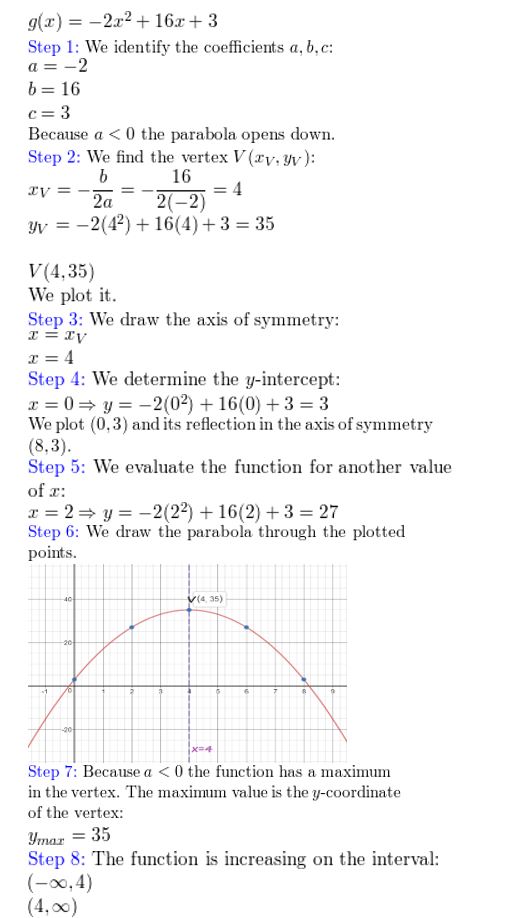
Question 8.
h(10) = (x – 3)(x + 7)

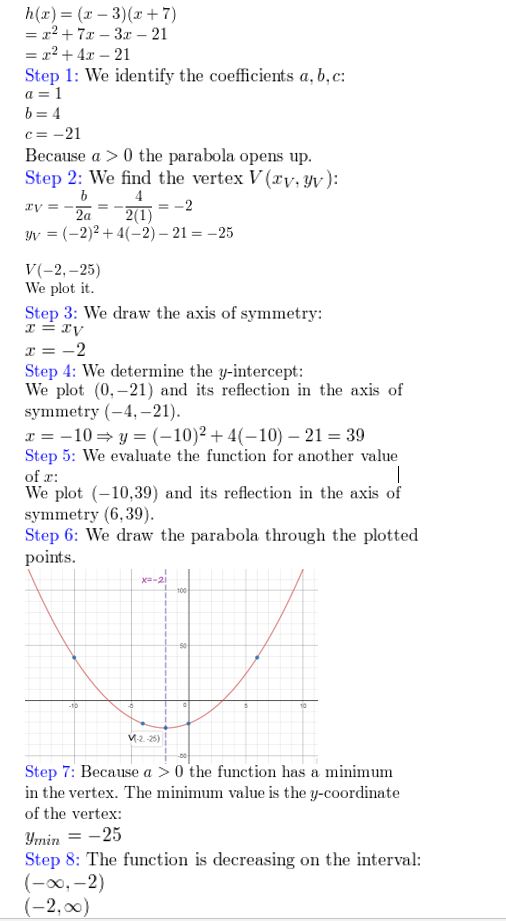
Question 9.
Y'all can make a solar hot-dog cooker by shaping foil-lined cardboard into a parabolic trough and passing a wire through the focus of each end piece. For the trough shown, how far from the bottom should the wire exist placed?

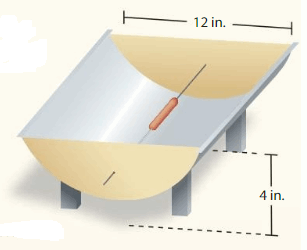
Question x:

Graph the equation 36y = ten^two. Place the focus, directrix, and axis of symmetry.

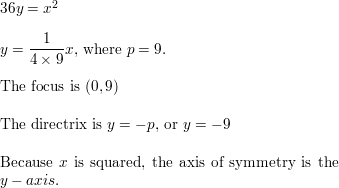
Write an equation of the parabola with the given characteristics.

Question eleven.
vertex: (0, 0)
directrix: x = two

Question 12.
focus: (ii, 2)
vertex: (2, half dozen)

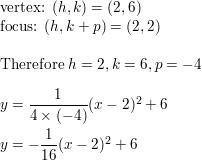
Write an equation for the parabola with the given characteristics.

Question thirteen.
passes through (i, 12) and has vertex (10, -4)

Question 14.
passes through (4, 3) and has x-intercepts of -one and 5

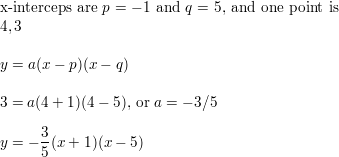
Question 15.
passes through (-2, vii), (1, ten), and (2, 27)

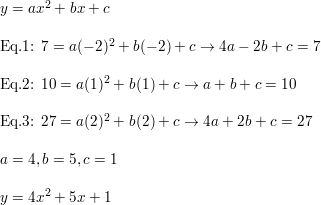
Question 16.
The table shows the heights y of a dropped object after x seconds. Verify that the data bear witness a quadratic relationship. Write a role that models the data. How long is the object in the air?

Quadratic Functions Chapter Exam

Question 1.
A parabola has an axis of symmetry y= 3 and passes through the point (2, 1). Find some other point that lies on the graph of the parabola. Explicate your reasoning.

Question 2.
Let the graph of g be a translation ii units left and i unit downward, followed by a reflection in the y-centrality of the graph of f(x) = (2x + 1)^two – 4. Write a rule for thou.

Question 3.
Identify the focus, directrix, and centrality of symmetry of x = 2y^two. Graph the equation.

Question 4.
Explain why a quadratic function models the data. And so use a linear system to find the model.

Write an equation of the parabola. Justify your answer.

Question 5.

Question six.

Question 7.

Question viii.
A surfboard shop sells 40 surfboards per month when it charges $500 per surfboard. Each time the shop decreases the toll by $x, it sells 1 additional surfboard per month. How much should the shop charge per surfboard to maximize the corporeality of money earned? What is the maximum corporeality the shop tin can earn per month? Explicate.

Question nine.
Graph f(x) = 8x² – 4x+ iii. Characterization the vertex and axis of symmetry. Depict where the role is increasing and decreasing.

Question ten.
Sunfire is a machine with a parabolic cross section used to collect solar energy. The Sun'due south rays are reflected from the mirrors toward two boilers located at the focus of the parabola. The boilers produce steam that powers an alternator to produce electricity.
a. Write an equation that represents the cross section of the dish shown with its vertex at (0, 0).
b. What is the depth of Sunfire? Justify your answer.

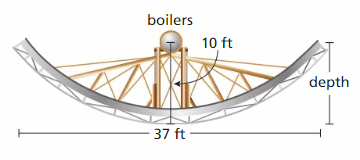
Question 11.
In 2011, the toll of gold reached an all-fourth dimension high. The table shows the prices (in dollars per troy ounce) of gilded each year since 2006 (t = 0 represents 2006). Discover a quadratic part that best models the data. Utilise the model to predict the price of gold in the year 2016.

Quadratic Functions Cumulative Assessment

Question 1.
You and your friend are throwing a football game. The parabola shows the path of your friend's throw, where x is the horizontal distance (in anxiety) and y is the corresponding height (in feet). The path of your throw can be modeled by h(x) = −16x² + 65x + 5. Cull the correct inequality symbol to indicate whose throw travels college. Explain your reasoning.

Question 2.
The function thou(x) = \(\frac{1}{ii}\)∣10 − 4 ∣ + iv is a combination of transformations of f(x) = | 10|. Which combinations describe the transformation from the graph of f to the graph of 1000?
A. translation 4 units right and vertical compress by a factor of \(\frac{1}{2}\), followed by a translation 4 units up
B. translation 4 units right and iv units up, followed past a vertical shrink past a factor of \(\frac{1}{2}\)
C. vertical compress by a factor of \(\frac{1}{ii}\) , followed by a translation 4 units upwards and 4 units right
D. translation 4 units correct and 8 units up, followed by a vertical shrink by a factor of \(\frac{one}{2}\)

Question 3.
Your school decides to sell tickets to a dance in the school cafeteria to raise money. In that location is no fee to use the cafeteria, simply the DJ charges a fee of $750. The table shows the profits (in dollars) when x students attend the dance.

a. What is the cost of a ticket?
b. Your school expects 400 students to attend and finds another DJ who only charges $650. How much should your school charge per ticket to still make the same profit?
c. Your school decides to accuse the amount in part (a) and use the less expensive DJ. How much more coin volition the school raise?

Question 4.
Order the following parabolas from widest to narrowest.
A. focus: (0, −three); directrix: y = 3
B. y = \(\frac{one}{16}\)x² + four
C. x = \(\frac{1}{8}\)y²
D. y = \(\frac{1}{four}\)(ten − 2)² + 3

Question 5.
Your friend claims that for g(10) = b, where b is a real number, there is a transformation in the graph that is impossible to find. Is your friend correct? Explain your reasoning.

Question 6.
Allow the graph of 1000 correspond a vertical stretch and a reflection in the x-axis, followed by a translation left and down of the graph of f(x) = 10^two. Use the tiles to write a rule for one thousand.

Question vii.
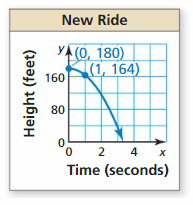
Two assurance are thrown in the air. The path of the starting time ball is represented in the graph. The 2d ball is released 1.5 feet higher than the showtime ball and afterwards iii seconds reaches its maximum height 5 anxiety lower than the first ball.

a. Write an equation for the path of the second ball.
b. Do the balls hit the footing at the same time? If so, how long are the balls in the air? If non, which ball hits the ground offset? Explain your reasoning.

Question 8.
Let the graph of k be a translation 3 units right of the graph of f. The points (−i, 6), (three, 14), and (half-dozen, 41) lie on the graph of f. Which points prevarication on the graph of g?
A. (2, 6)
B. (2, eleven)
C. (vi, 14)
D. (6, xix)
East. (9, 41)
F. (9, 46)

Question 9.
Gym A charges $10 per month plus an initiation fee of $100. Gym B charges $30 per month, merely due to a special promotion, is not currently charging an initiation fee.
a. Write an equation for each gym modeling the total price y for a membership lasting x months.
b. When is it more economical for a person to choose Gym A over Gym B?
c. Gym A lowers its initiation fee to $25. Describe the transformation this change represents and how it affects your decision in part (b).

caseythounfor.blogspot.com

Source: https://ccssmathanswers.com/big-ideas-math-algebra-2-answers-chapter-2/

Share this post